Dijkstra's algorithm. Search for optimal routes on the graph
Of the many search algorithms for shortest routes on a graph, on Habré, I found only a description of the Floyd-Worschall algorithm. This algorithm finds the shortest paths between all the vertices of the graph and their length. In this article I will describe the principle of operation of the Dijkstra algorithm, which finds the optimal routes and their length between one particular vertex (source) and all the other vertices of the graph. The disadvantage of this algorithm is that it will work incorrectly if the graph has arcs of negative weight.
For example, take the following directed graph G:
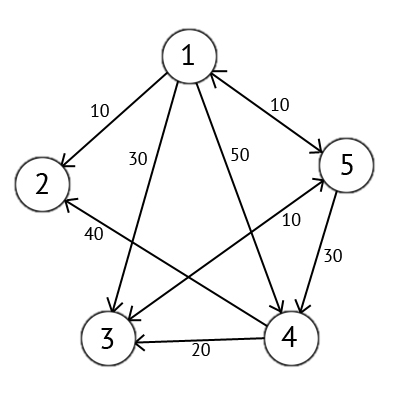
')
We can present this graph as a matrix C:
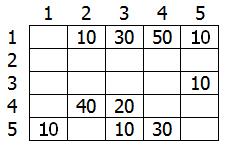
Let's take vertex 1 as the source. This means that we will search for the shortest routes from vertex 1 to vertices 2, 3, 4 and 5.
This algorithm iterates through all the vertices of the graph and assigns labels to them, which are the known minimum distance from the vertex of the source to a particular vertex. Consider this algorithm by example.
Let's assign the 1st vertex a label equal to 0, because this vertex is the source. The remaining vertices will be assigned labels equal to infinity.
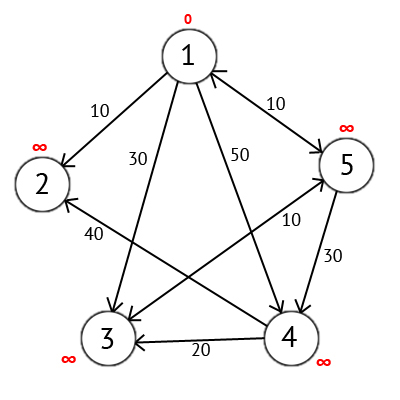
Next, choose a vertex W that has a minimal label (now it is vertex 1) and consider all vertices at which from vertex W there is a path that does not contain vertices of mediators. Assign a label equal to the sum of the W mark and paths from W to the vertex under consideration to each of the vertices considered, but only if the resulting sum is less than the previous mark value. If the amount is not less, then leave the previous label unchanged.
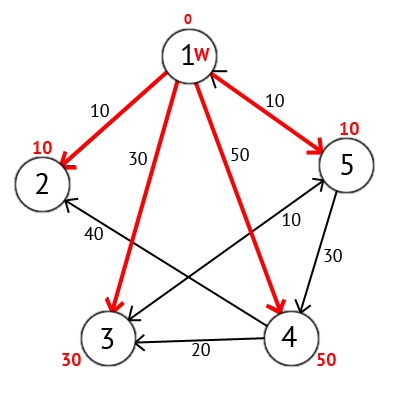
After we have considered all the vertices that have a direct path from W, we mark the top of W as visited, and choose from those that have not yet visited that which has the minimum value of the label, it will be the next peak of W. In this case, this is top 2 or 5. If there are several vertices with the same labels, then it does not matter which of them we choose as W.
We will choose vertex 2. But there is not a single outgoing path from it, so we immediately mark this vertex as visited and proceed to the next vertex with the minimum mark. This time only vertex 5 has a minimum mark. Consider all the vertices in which there are direct paths from 5, but which are not yet marked as visited. Again, we find the sum of the label of the vertex W and the weight of the edge from W to the current vertex, and if this sum is less than the previous label, then we replace the value of the label with the resulting sum.
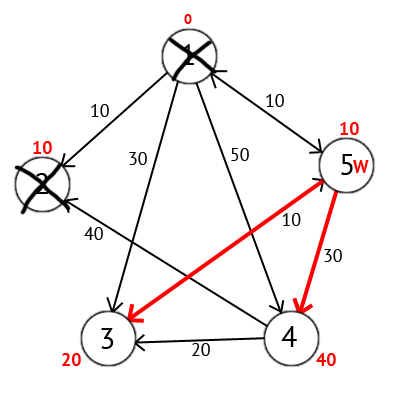
Based on the picture, we can see that the labels of the 3rd and 4th peaks are smaller, that is, a shorter route to these peaks from the top of the source was found. Next, mark the 5th vertex as visited and select the next vertex that has the minimum mark. Repeat all the above actions as long as there are unvisited vertices.
After completing all the actions we get the following result:
There is also a vector P, based on which you can build the shortest routes. By the number of elements, this vector is equal to the number of vertices in the graph. Each element contains the last intermediate vertex on the shortest path between the source vertex and the final vertex. At the beginning of the algorithm, all elements of the vector P are equal to the top of the source (in our case, P = {1, 1, 1, 1, 1}). Next, at the stage of recalculation of the label value for the considered vertex, if the label of the considered vertex changes to a smaller one, we write the value of the current vertex W to the array P. For example: the 3rd vertex had a label with the value “30”, with W = 1. Further, at W = 5, the label of the 3rd vertex has changed to “20”, therefore we will write the value in the vector - [3] = 5. Also, when W = 5, the value of the label at the 4th vertex has changed (it was “50”, it has become “40”), so the value of W - P [4] = 5 must be assigned to the 4th element of the vector P. As a result, we obtain the vector P = {1, 1, 5, 5, 1}.
Knowing that the last intermediate vertex on the path between the source and the final vertex is recorded in each element of the vector P, we can also get the shortest route.
For example, take the following directed graph G:

')
We can present this graph as a matrix C:

Let's take vertex 1 as the source. This means that we will search for the shortest routes from vertex 1 to vertices 2, 3, 4 and 5.
This algorithm iterates through all the vertices of the graph and assigns labels to them, which are the known minimum distance from the vertex of the source to a particular vertex. Consider this algorithm by example.
Let's assign the 1st vertex a label equal to 0, because this vertex is the source. The remaining vertices will be assigned labels equal to infinity.

Next, choose a vertex W that has a minimal label (now it is vertex 1) and consider all vertices at which from vertex W there is a path that does not contain vertices of mediators. Assign a label equal to the sum of the W mark and paths from W to the vertex under consideration to each of the vertices considered, but only if the resulting sum is less than the previous mark value. If the amount is not less, then leave the previous label unchanged.

After we have considered all the vertices that have a direct path from W, we mark the top of W as visited, and choose from those that have not yet visited that which has the minimum value of the label, it will be the next peak of W. In this case, this is top 2 or 5. If there are several vertices with the same labels, then it does not matter which of them we choose as W.
We will choose vertex 2. But there is not a single outgoing path from it, so we immediately mark this vertex as visited and proceed to the next vertex with the minimum mark. This time only vertex 5 has a minimum mark. Consider all the vertices in which there are direct paths from 5, but which are not yet marked as visited. Again, we find the sum of the label of the vertex W and the weight of the edge from W to the current vertex, and if this sum is less than the previous label, then we replace the value of the label with the resulting sum.

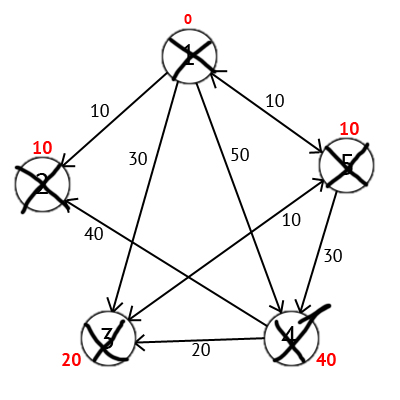
Based on the picture, we can see that the labels of the 3rd and 4th peaks are smaller, that is, a shorter route to these peaks from the top of the source was found. Next, mark the 5th vertex as visited and select the next vertex that has the minimum mark. Repeat all the above actions as long as there are unvisited vertices.
After completing all the actions we get the following result:

There is also a vector P, based on which you can build the shortest routes. By the number of elements, this vector is equal to the number of vertices in the graph. Each element contains the last intermediate vertex on the shortest path between the source vertex and the final vertex. At the beginning of the algorithm, all elements of the vector P are equal to the top of the source (in our case, P = {1, 1, 1, 1, 1}). Next, at the stage of recalculation of the label value for the considered vertex, if the label of the considered vertex changes to a smaller one, we write the value of the current vertex W to the array P. For example: the 3rd vertex had a label with the value “30”, with W = 1. Further, at W = 5, the label of the 3rd vertex has changed to “20”, therefore we will write the value in the vector - [3] = 5. Also, when W = 5, the value of the label at the 4th vertex has changed (it was “50”, it has become “40”), so the value of W - P [4] = 5 must be assigned to the 4th element of the vector P. As a result, we obtain the vector P = {1, 1, 5, 5, 1}.
Knowing that the last intermediate vertex on the path between the source and the final vertex is recorded in each element of the vector P, we can also get the shortest route.
Source: https://habr.com/ru/post/111361/
All Articles