Some ideas of writing an artificial intellect for chess
Unfortunately, there are no better algorithms for chess than the search for so many positions. True, the brute force order (and not one) is optimized, but still it is a big brute force. To search for a reciprocal move, a tree is built with the initial move at the root, the edges are constructed with moves-answers and nodes - with new positions.
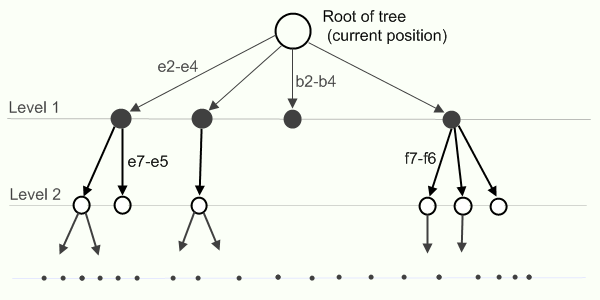
As in the elementary algorithms, the next move is chosen to be explained simply. On your turn, you choose such a move (in your opinion) that will bring the greatest benefit (maximizes your benefit), and the opponent in her next move tries to choose the move that will bring him the most benefit (maximizes his benefit and minimizes yours). An algorithm with this principle is called minimax. At each stage, you assign each position in the tree an assessment of the position (more on this later) and maximize it during your move, and minimize it during the opponent’s move. The algorithm during operation must go through all the nodes of the tree (that is, all possible gaming positions in the game), that is, it is completely unsuitable in time.
His next improvement is alpha-beta pruning (branch and bound method).
From the name it follows that the algorithm is cut off by some two parameters - alpha and beta. The main idea of the cut-off is that now we will keep the cut-off interval (lower and upper bounds - alpha and beta, respectively - your KO) and estimates of all nodes that do not fall into the interval from below, we will not consider (since they are not affect the result - it's just the worst moves than the one already found), and the interval itself will be narrowed as the best moves are found. Although the alpha-beta cut-off is much better than the minix, yet its running time is also very large. If we assume that there are approximately 40 different moves in the middle of a game, then the algorithm time can be estimated as O (40 ^ P), where P is the depth of the move tree. Of course, with a minimax there can be such a sequence of consideration of moves, when we will not do any clippings, then the alpha-beta pruning will simply turn into a minimax. At best, using the alpha-beta cut-off, you can avoid checking the root from among all the moves in the minimax. In order to avoid a long time of work (with such an O-great complexity of the algorithm), a search in the tree is done for some fixed value and a node is evaluated there. This assessment is a very great approximation to the actual assessment of the node (that is, going through the end of the tree, and there the result is “won, lost, draw”). As for the evaluation of a node, there is just a pile of various methods (you can read in the links at the end of the article). In short, naturally, I count the player’s material (according to one system - whole numbers, pawn - 100, knight and bishop - 300, rook - 500, queen - 900; according to another system - valid in parts from one) + position on the board player As for the position, here one of the nightmares of writing chess begins, since the speed of the program will mainly depend on the evaluation function and, more precisely, on the assessment of the position. There is already someone in that much. For a paired tour to player +, for covering the king with his pawns +, for a pawn near the other end of the board +, etc., and hanging position, the open king, etc., minus the position. etc. - Factors can write a bunch. Here, to assess the position in the game, an assessment of the position of the player is made, which makes a move, and the assessment of the corresponding position of the opponent is subtracted from it. As they say, one photo is sometimes better than a thousand words, and maybe a piece of code in pseudo C # will also be better than an explanation:
')
I think some explanations about the code will not be superfluous:
An example of using the method:
where MateValue is quite a large number.
The max_depth parameter is the maximum depth to which the algorithm will go down in the tree. It should be borne in mind that pseudocode is purely demonstrative, but quite working.
Instead of coming up with a new algorithm, people promoting alpha-beta clipping came up with many different heuristics. A heuristic is just a small hack that sometimes makes a very big speed gain. There is a lot of heuristics for chess, you can’t count them all. I will give only the main ones, the rest can be found in the links at the end of the article.
First, a very well-known “zero move” heuristic is applied. In a quiet position, the opponent is given two turns instead of one, and after that they look at the tree to a depth (depth-2), and not (depth-1). If, after evaluating such a subtree, it turns out that the current player still has an advantage, then it makes no sense to consider the subtree further, since after his next move the player will only make his position better. Since brute force polynomial, the gain in speed is palpable. Sometimes it happens that the enemy aligns his advantage, then we must consider the entire subtree to the end. It’s not necessary to make an empty move (for example, when one of the kings is under a check, in zugzwang or endgame).
Further, the idea is used first to make a move in which there will be a capture of the opponent’s piece that made the last move. Since almost all the moves during the brute force search are not very reasonable, such an idea would greatly narrow the search box at the beginning, thereby cutting off many unnecessary moves.
Also known is the heuristics of history or the service of the best moves . During the search, the best moves at this level of the tree are preserved, and when considering a position, you can first try to make such a move for a given depth (based on the idea that at equal depths in the tree very often the same best moves are made).
It is known that this kind of caching of moves improved the performance of the Soviet program Kaiss by 10 times.
There are also some ideas about generating moves. First consider winning takes, that is, such a take, when a figure with a lower score beats a figure with a higher score. Then promotions are considered (when the pawn on the other end of the board can be replaced with a stronger piece), then equal takes and then moves from the history heuristics cache. The remaining moves can be sorted for control of the board or some other criterion.
Everything would be fine if alpha-beta pruning guaranteed would give the best answer. Even considering a long time to bust. But it was not there. The problem is that after a search for a fixed value, the position is assessed and that’s it, and as it turned out, in some game positions the search cannot be stopped. After many attempts, it turned out that the search can only be stopped in calm positions. Therefore, in the main search, an additional search was added, in which only captures, promotions and shahs (called forced search ) are considered. We also noticed that some positions with exchanges in the middle should also be considered deeper. So there were ideas about extensions and reductions , that is, recesses and shortenings of the search tree. For ditches, the most suitable positions are the type of endgame with pawns, departure from the shah, exchange of a piece in the middle of a brute force, etc. “Absolutely calm” positions are suitable for shortening. In the Soviet program of Kaiss, the forced search was a bit special — there, immediately after taking, during the search, the forced search began and its depth was not limited (since after a while it would exhaust itself in a calm position).
In the words of Anthony Hoar : " Premature of evil in programming. " (Note: for those who believe that this quote belongs to Knut, there are interesting discussions here and here ). In chess, where there will be a relatively large depth of recursion, it is necessary to think about optimizations, but very carefully.
There are some general ideas here too:
The article used information from some resources:
PS The whole theory was used by me in practice and for some time there was a simple PHP rest-web service for online chess + C # program (used .NET Remoting for a network game), but now the site is not working and when I have time I want to transfer to RubyOnRails.
PPS Who cares - the project now lives on Google code and upgrade when I have time. Who wants the code of the previous version - I can send.

As in the elementary algorithms, the next move is chosen to be explained simply. On your turn, you choose such a move (in your opinion) that will bring the greatest benefit (maximizes your benefit), and the opponent in her next move tries to choose the move that will bring him the most benefit (maximizes his benefit and minimizes yours). An algorithm with this principle is called minimax. At each stage, you assign each position in the tree an assessment of the position (more on this later) and maximize it during your move, and minimize it during the opponent’s move. The algorithm during operation must go through all the nodes of the tree (that is, all possible gaming positions in the game), that is, it is completely unsuitable in time.
His next improvement is alpha-beta pruning (branch and bound method).
From the name it follows that the algorithm is cut off by some two parameters - alpha and beta. The main idea of the cut-off is that now we will keep the cut-off interval (lower and upper bounds - alpha and beta, respectively - your KO) and estimates of all nodes that do not fall into the interval from below, we will not consider (since they are not affect the result - it's just the worst moves than the one already found), and the interval itself will be narrowed as the best moves are found. Although the alpha-beta cut-off is much better than the minix, yet its running time is also very large. If we assume that there are approximately 40 different moves in the middle of a game, then the algorithm time can be estimated as O (40 ^ P), where P is the depth of the move tree. Of course, with a minimax there can be such a sequence of consideration of moves, when we will not do any clippings, then the alpha-beta pruning will simply turn into a minimax. At best, using the alpha-beta cut-off, you can avoid checking the root from among all the moves in the minimax. In order to avoid a long time of work (with such an O-great complexity of the algorithm), a search in the tree is done for some fixed value and a node is evaluated there. This assessment is a very great approximation to the actual assessment of the node (that is, going through the end of the tree, and there the result is “won, lost, draw”). As for the evaluation of a node, there is just a pile of various methods (you can read in the links at the end of the article). In short, naturally, I count the player’s material (according to one system - whole numbers, pawn - 100, knight and bishop - 300, rook - 500, queen - 900; according to another system - valid in parts from one) + position on the board player As for the position, here one of the nightmares of writing chess begins, since the speed of the program will mainly depend on the evaluation function and, more precisely, on the assessment of the position. There is already someone in that much. For a paired tour to player +, for covering the king with his pawns +, for a pawn near the other end of the board +, etc., and hanging position, the open king, etc., minus the position. etc. - Factors can write a bunch. Here, to assess the position in the game, an assessment of the position of the player is made, which makes a move, and the assessment of the corresponding position of the opponent is subtracted from it. As they say, one photo is sometimes better than a thousand words, and maybe a piece of code in pseudo C # will also be better than an explanation:
')
enum CurentPlayer {Me, Opponent}; public int AlphaBetaPruning (int alpha, int beta, int depth, CurrentPlayer currentPlayer) { // value of current node int value; // count current node ++nodesSearched; // get opposite to currentPlayer CurrentPlayer opponentPlayer = GetOppositePlayerTo(currentPlayer); // generates all moves for player, which turn is to make move / /moves, generated by this method, are free of moves // after making which current player would be in check List<Move> moves = GenerateAllMovesForPlayer(currentPlayer); // loop through the moves foreach move in moves { MakeMove(move); ++ply; // If depth is still, continue to search deeper if (depth > 1) value = -AlphaBetaPruning (-beta, -alpha, depth - 1, opponentPlayer); else // If no depth left (leaf node), evalute that position value = EvaluatePlayerPosition(currentPlayer) - EvaluatePlayerPosition(opponentPlayer); RollBackLastMove(); --ply; if (value > alpha) { // This move is so good that caused a cutoff of rest tree if (value >= beta) return beta; alpha = value; } } if (moves.Count == 0) { // if no moves, than position is checkmate or if (IsInCheck(currentPlayer)) return (-MateValue + ply); else return 0; } return alpha; } I think some explanations about the code will not be superfluous:
- GetOppositePlayerTo () simply changes CurrentPlayer.Me to CurrentPlayer.Opponent and vice versa
- MakeMove () makes the next move from the list of moves.
- ply - a global variable (part of the class), which keeps in itself the number of half-moves made at a given depth
An example of using the method:
{ ply = 0; nodesSearched = 0; int score = AlphaBetaPruning (-MateValue, MateValue, max_depth, CurrentPlayer.Me); } where MateValue is quite a large number.
The max_depth parameter is the maximum depth to which the algorithm will go down in the tree. It should be borne in mind that pseudocode is purely demonstrative, but quite working.
Instead of coming up with a new algorithm, people promoting alpha-beta clipping came up with many different heuristics. A heuristic is just a small hack that sometimes makes a very big speed gain. There is a lot of heuristics for chess, you can’t count them all. I will give only the main ones, the rest can be found in the links at the end of the article.
First, a very well-known “zero move” heuristic is applied. In a quiet position, the opponent is given two turns instead of one, and after that they look at the tree to a depth (depth-2), and not (depth-1). If, after evaluating such a subtree, it turns out that the current player still has an advantage, then it makes no sense to consider the subtree further, since after his next move the player will only make his position better. Since brute force polynomial, the gain in speed is palpable. Sometimes it happens that the enemy aligns his advantage, then we must consider the entire subtree to the end. It’s not necessary to make an empty move (for example, when one of the kings is under a check, in zugzwang or endgame).
Further, the idea is used first to make a move in which there will be a capture of the opponent’s piece that made the last move. Since almost all the moves during the brute force search are not very reasonable, such an idea would greatly narrow the search box at the beginning, thereby cutting off many unnecessary moves.
Also known is the heuristics of history or the service of the best moves . During the search, the best moves at this level of the tree are preserved, and when considering a position, you can first try to make such a move for a given depth (based on the idea that at equal depths in the tree very often the same best moves are made).
It is known that this kind of caching of moves improved the performance of the Soviet program Kaiss by 10 times.
There are also some ideas about generating moves. First consider winning takes, that is, such a take, when a figure with a lower score beats a figure with a higher score. Then promotions are considered (when the pawn on the other end of the board can be replaced with a stronger piece), then equal takes and then moves from the history heuristics cache. The remaining moves can be sorted for control of the board or some other criterion.
Everything would be fine if alpha-beta pruning guaranteed would give the best answer. Even considering a long time to bust. But it was not there. The problem is that after a search for a fixed value, the position is assessed and that’s it, and as it turned out, in some game positions the search cannot be stopped. After many attempts, it turned out that the search can only be stopped in calm positions. Therefore, in the main search, an additional search was added, in which only captures, promotions and shahs (called forced search ) are considered. We also noticed that some positions with exchanges in the middle should also be considered deeper. So there were ideas about extensions and reductions , that is, recesses and shortenings of the search tree. For ditches, the most suitable positions are the type of endgame with pawns, departure from the shah, exchange of a piece in the middle of a brute force, etc. “Absolutely calm” positions are suitable for shortening. In the Soviet program of Kaiss, the forced search was a bit special — there, immediately after taking, during the search, the forced search began and its depth was not limited (since after a while it would exhaust itself in a calm position).
In the words of Anthony Hoar : " Premature of evil in programming. " (Note: for those who believe that this quote belongs to Knut, there are interesting discussions here and here ). In chess, where there will be a relatively large depth of recursion, it is necessary to think about optimizations, but very carefully.
There are some general ideas here too:
- debut library (debut theory in chess is very advanced - Wiki + Database )
- endgame library (likewise there are many endgame databases)
- iterative deepening + caching : the idea is to do a search first to a depth of 1, then 2, 3, and so on. At the same time maintain this position, its best course, depth, or something else in some kind of hash table. The whole essence of iterative grooves is that the result of unfinished iteration cannot be used (then it is better to do an incomplete exhaustion to a shallower depth) and when iterating to a greater depth, you can use the results of a exhaustive search to a shallower depth. It even turns out that brute force to a depth of 1 to 6 is performed faster than brute force immediately to a depth of 6.
The article used information from some resources:
- Rebel - Programmer Stuff - an article about the Rebel program (very valuable ideas and solutions)
- Chess Tree Search - General Chess Programming Ideas
- Forum about the search for an algorithm for chess by one person
- Site of the working group on artificial intelligence
- How computers play chess - an article in Habré
- Chess Program Sources - available sources of many chess programs
PS The whole theory was used by me in practice and for some time there was a simple PHP rest-web service for online chess + C # program (used .NET Remoting for a network game), but now the site is not working and when I have time I want to transfer to RubyOnRails.
PPS Who cares - the project now lives on Google code and upgrade when I have time. Who wants the code of the previous version - I can send.
Source: https://habr.com/ru/post/111210/
All Articles