Direct Fuzzy Inference

Introduction

In 1965, L.Zade's work entitled “Fuzzy sets” was published in the magazine “Information and Control”. This name is translated into Russian as fuzzy sets . The motive was the need to describe such phenomena and concepts that have a multi-valued and inaccurate character. The previously known mathematical methods that used classical set theory and two-valued logic did not allow solving problems of this type.



With the help of fuzzy sets, you can formally define inaccurate and ambiguous concepts, such as "high temperature" or "big city". To formulate the definition of a fuzzy set, it is necessary to specify a so-called area of ​​reasoning. For example, when we estimate the speed of a car, we will limit ourselves to the range X = [0, Vmax], where Vmax is the maximum speed that a car can develop. It must be remembered that X is a clear set.
')

Basic concepts

The fuzzy set A in some non-empty space X is the set of pairs

Where

- membership function of a fuzzy set A. This function assigns to each element x the degree of its membership to a fuzzy set A.

Continuing the previous example, consider three inaccurate statements:
- “Low car speed”;
- “Average vehicle speed”;
- "High speed car."
The figure shows fuzzy sets corresponding to the above formulations using membership functions.

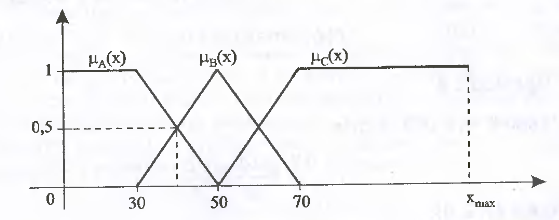
At a fixed point X = 40km / h. the membership function of the fuzzy set "low speed car" takes the value of 0.5. The same value is assumed by the accessory function of the fuzzy set “average vehicle speed”, whereas for the set “high vehicle speed” the value of the function at this point is 0.

The function T of two variables T: [0, 1] x [0, 1] -> [0, 1] is called a T-norm if:
- is not increasing with respect to both arguments: T (a, c) <T (b, d) for a <b, c <d;
- is commutative: T (a, b) = T (b, a);
- satisfies the condition of connectedness: T (T (a, b), c) = T (a, T (b, c));
- satisfies the boundary conditions: T (a, 0) = 0, T (a, 1) = a.

Direct fuzzy output

By fuzzy inference is meant a process in which some consequences are obtained from fuzzy premises, possibly also fuzzy. Approximate reasoning underlies the ability of a person to understand natural language, to understand handwriting, to play games that require mental effort, in general, to make decisions in a complex and not fully defined environment. This ability of reasoning in qualitative, inaccurate terms distinguishes the human intellect from the intellect of the computer.

The main rule of inference in traditional logic is the rule of modus ponens, according to which we judge the truth of the statement B by the truth of statements A and A -> B. For example, if A is the statement “Stepan is an astronaut”, B is the statement “Stepan flies into space” , if the statements “Stepan is an astronaut” and “If Stepan is a cosmonaut, then he flies into space,” then the statement “Stepan flies into space” is true.

However, unlike traditional logic, the main tool of fuzzy logic is not the modus ponens rule, but the so-called compositional inference rule, of which the modus ponens rule is a very special case.

Suppose that there is a curve y = f (x) and the value x = a is given. Then from the fact that y = f (x) and x = a, we can conclude that y = b = f (a).

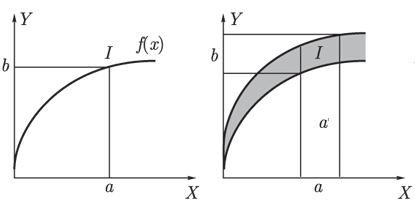
Let us now generalize this process, assuming that a is an interval, and f (x) is a function whose values ​​are intervals. In this case, to find the interval y = b corresponding to the interval a, we first construct the set a 'with base a and find its intersection I with the curve, whose values ​​are intervals. Then we project this intersection onto the OY axis and obtain the desired value of y as an interval b. Thus, from the fact that y = f (x) and x = A is a fuzzy subset of the OX axis, we get the value of y in the form of a fuzzy subset B of the OY axis.

Let U and V be two universal sets with basic variables u and v, respectively. Let A and F be fuzzy subsets of the sets U and U x V. Then the compositional inference rule states that the fuzzy sets A and F imply the fuzzy set B = A * F.

Let A and B be fuzzy statements and m (A), m (B) the corresponding membership functions. Then the implications A -> B will correspond to a certain membership function m (A -> B). By analogy with traditional logic, it can be assumed that

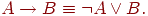
Then

However, this is not the only generalization of the implication operator, there are others.

Implementation

To implement the direct fuzzy inference method, we need to choose the implication operator and the T-norm.
Starting the T-norm will be the minimum function:

1. def t_norm (v1, v2): return min (v1, v2)
2. def t_norm (v1, v2): return min (v1, v2)

and the operator of the implication will be the Gödel function:

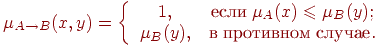
1. def impl (v1, v2):
2. '' ' <br/> Godel implication <br/> ' ''
3. if v1 <= v2:
4. return 1 . 0
5. else :
6. return v2

Input data will contain knowledge (fuzzy sets) and rules (implications), for example:
A = {(x1, 0.0), (x2, 0.2), (x3, 0.7), (x4, 1.0)}.
B = {(x1, 0.7), (x2, 0.4), (x3, 1.0), (x4, 0.1)}.
A => B.

The implication will be represented as a Cartesian matrix, each element of which is calculated using the selected implication operator (in this example, the Gödel function):

1. def compute_impl (set1, set2):
2. '' ' <br/> Computing implication <br/> ' ''
3. relation = {}
4. for i in set1.items ():
5. relation [i] = {}
6. for j in set2.items ():
7. v1 = set1.value (i)
8. v2 = set2.value (j)
9. relation [i] [j] = impl (v1, v2)
10. return relation

For the data above, this will be:
Conclusion:
A => B.
x1 x2 x3 x4
x1 1.0 1.0 1.0 1.0
x2 1.0 1.0 1.0 0.1
x3 1.0 0.4 1.0 0.1
x4 0.7 0.4 1.0 0.1

Further, as a result of the output a new set is obtained:

1. def conclusion (set, relation):
2. '' ' <br/> Conclusion <br/> ' ''
3. conl_set = []
4. for i in relation:
5. l = []
6. for j in relation [i]:
7. v_set = set. value (i)
8. v_impl = relation [i] [j]
9. l.append (t_norm (v_set, v_impl))
10. value = max (l)
11. conl_set.append ((i, value))
12. return conl_set

Result:
B '= {(x1, 1.0), (x2, 0.7), (x3, 1.0), (x4, 0.7)}.

Sources

• Rutkovskaya D., Pilinsky M., Rutkovsky L. Neural networks, genetic algorithms and fuzzy systems: Trans. from polish I.D. Rudinsky. - M .: Hotline - Telecom, 2006. - 452 pp., Ill.
• Zadeh LA Fuzzy Sets, Information and Control, 1965, vol. 8, s. 338-353