Geekly Articles each Day
⬆️ ⬇️

TAU-Darwinism

Foreword



“Cyber ​​warden Uncle Fedya is exactly three bears by force,” said Paul, removing an adjustment block from the bowels of the cyber warden. “I already know Fedyu here.” Pleasant so freckled. A very, very aseptic young man. Is this not your relative?


Arkady and Boris Strugatsky (Noon. XXII century).



The article is devoted to the question of the applicability of genetic algorithms to the problem of identifying a dynamic system.

Updated: published continuation of TAU-Darwinism: implementation on Ruby





Introduction



Identifying the structure of a mathematical model, as part of analyzing physical systems, means finding an algebraic expression (equation) describing the physical model of an object. Many systems identification methods are parametric, i.e. The structure of the model of the object being identified is determined and the values ​​of the parameters of this model are calculated using the specified formulas. This article presents a method for selecting the optimal mathematical model of an object using genetic programming.

The advantage of the GA in this matter is that these algorithms do not limit the list of systems that can be identified with their help and can be applied to any data set representing the “input-output” system. When using GA there is no need to pre-determine the structure of the identified object. The optimal structure of the model will be found in the process of evolution of a randomly generated population of individuals (models).

')

Terminology







Identification object



A non-homogeneous differential equation will be considered as the initial mathematical model of the object being identified. For simplicity, a second degree differential equation will be used as an example:

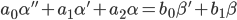(one)


In the formula (1) "" "(apostrophe) means the time derivative - the operator d / dt; α is the output coordinate (for example, the deviation of the sensitive element from the equilibrium position); β - input impact, control (for example, the force acting on the SE and leading to its deviation).

In the operator record form (s = d / dt), this equation will have the form:

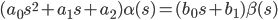(2)


According to the expression (2) is the transfer function - the ratio of the output to the input:

(3)


In (3), the denominator is the “characteristic equation” of the system. It defines the main characteristics of the dynamics (for example, stability). The roots of this equation are called the poles of a dynamical system. The roots of the numerator are called zeros of the dynamical system.

The transfer function (3) can be rewritten in the form of a fraction, the numerator and denominator of which are the products of two- and three-terms:

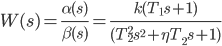(four)


In this case, both the numerator and the denominator contain one polynomial each, but in the general case there will be several for equations of order 4 or more. Moreover, each of them corresponds to a point on the complex plane. A binomial point corresponds to a point on the real axis, and a three-member corresponds to a point not lying on the real axis. The last statement is true only in the case when the trinomial has only two complex conjugate roots. Otherwise, this trinomial can be represented as a product of two binomials.

In expression (4), the “T” coefficients are time constants, and the η coefficient is the damping decrement coefficient (it is also an indicator of oscillation or the coefficient of damping).



Genetic coding



To write a mathematical model of an identifiable object in the form (2) it is convenient to use a gene coding scheme with real numbers. Moreover, the number of alleles of each gene will be determined by the bit depth (the number of bits of the binary representation) of real numbers in the software implementation of the algorithms.

Let a mathematical model of the form (2) encode two chromosomes - one for entry (right side) and the other for exit (left side). Genes in chromosomes correspond to one of the terms in equations (2). The value of the gene is equal to the value of the coefficient of the variables in the equations. In this case, the number of genes in the chromosomes can be any. When using this approach, you can encode the system with the input and output of any order. As a result, this will allow to encode a dynamic system with any topology and any number of feedbacks. You only need to follow the rule of physical realizability - the order of entry is less than or equal to the order of exit.

The disadvantage of this approach is that it complicates the monitoring of the characteristics of the dynamics. If we compare (3) and (4), then it is easy to notice that each of the coefficients in (3) is a combination of several coefficients in (4). Therefore, from the point of view of the synthesis of the optimal controller, it may be more advantageous to use the model entry in the form (4) even in the context of the GA . In this case, the genes will contain the value of the pole or zero of the PF , and this value will be complex. With this approach to identification using genetic programming, an increase in the stability of individuals in the population and the rate of convergence of the algorithm to the optimal result are expected.

Regardless of the choice of the PF record form when using coding with real (or complex) numbers, the chromosome will be an array of numbers. You can also enter binary encoding by specifying the quantization by level and converting real numbers to integers in binary representation (“Gray code” [2]). However, often in the transfer functions, the neighboring coefficients differ from each other by several orders of magnitude, therefore problems with accuracy may arise. Another binary coding method is logarithmic (also see [2]), in which the first two bits encode the signs of the number and the exponent of the power function, and the rest encode the value of the exponent itself. Using binary coding on the one hand will complicate the algorithm when using complex numbers, but on the other it will allow the use of classical genetic operators that require binary data representation.



Fitness function



One of the main concepts in the GA is the concept of "fitness function" or "fitness function." It shows how well the solution represented by this individual satisfies the conditions of the problem. In the context of the synthesis of the optimal regulator, the quality of regulation can be used as the main criterion for assessing the “fitness” of an individual; A good combination of the smoothness of the transition process and its duration. In the task of identification, the degree of approximation of the model’s response to the input to the response of the real (identifiable) object to the effect itself is more important. It is possible to estimate the degree of proximity by the mean-square criterion, calculating the standard deviation of the model response from the recorded output signal of the object being identified. In this case, the fitness function will be in the form of a formula for calculating the variance:

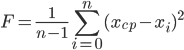(five)


In expression (5), n is the number of samples in the recorded output of the identifiable object; x cf is the arithmetic mean value of the deviation of the response of this individual from the output signal of the object being identified.

The procedure for calculating the "fitness" of an individual is as follows. First you need to decode the chromosome, i.e. based on the values ​​encrypted in it, first create a continuous transfer function (continuous-phase time function), and then make a discrete model convenient for carrying out numerical simulation. It is most convenient for me to use a discrete model in the state space [ 5 ].

The input identical to the input of the identified object is applied to the input of the compiled discrete model. Record the individual's reaction to this effect. In this case, the model of an individual is composed with a quantization period in time equal to the quantization period of the output signal of the object. Next, you need to use formula (5), previously subtracting, term by word, from the resulting array, the elements of the array with recording the output signal of the object, after which you can divide the unit by the resulting dispersion, if individuals with higher values ​​of the fitness function are considered more appropriate.

In addition, it is possible to introduce into the fitness function a special scaling (for example, exponential) so that the most ill-adapted individuals sift out more slowly. This needs to be done to maintain gene diversity at the proper level. It is also necessary to add an individual test for viability. As criteria for such an assessment, the following can be used:





Crossbreeding and mutation



The publication [2, p. 134] describes a single-point crossing algorithm. It consists in choosing a locus in which chromosomes will “stick together” and exchange the branches thus obtained between the chromosomes. The result is two chromosomes, each of which contains genes from both parents. You can create one individual for each of the chromosomes or only one individual for one of the chromosomes.

The same publication describes a multipoint method of crossing. The essence remains the same - sticking points are created and gene chains are recombined. The only difference is in the number of possible combinations of genes and, accordingly, in the number of the resulting combined chromosomes. Again, you can create several individuals (not necessarily for each of the chromosomes), but you can only one.

The gene exchange algorithm itself can be modified. If instead of a simple replacement of values ​​we use the calculation of a certain weighted average , then a similarity of the mechanism of gene competition ( dominant genes and recessive ones ) will be created. With the only difference that the dominance of genes will be determined by the fitness of the individual.

The mutation operator can be implemented by simply calculating a random value for a randomly selected gene, you can calculate a random increment to the current value of the gene, or you can invert a bit . The first method is undesirable, since the values ​​of the coefficients in the transfer functions can vary over a wide range, and changing the value of one coefficient from very small to large will lead to a sharp change in the value of the fitness function and loss of stability of the model. The same danger exists in a binary mutation - a change in the bit responsible for the sign of a number can lead to a loss of stability. Therefore, the most optimal in this case is the algorithm for calculating the random increment, reduced to the current value of the gene. This approach means that the range in which a random number is selected is proportional to the current value of the gene. The proportionality factor can be chosen equal to several units.



Population evolution



On page 211 in [2] the pseudo-code of population evolution is presented:





At each iteration step, standard genetic programming procedures are performed on individuals of the population: calculation of fitness functions, selection, crossing, mutation. For the evolution of the population as a whole, the selection procedure plays a key role. It depends on how fast and whether the population will move to a global optimum at all or will it be stuck in a local extremum. There are several approaches:



It should be noted that it is desirable to introduce a mechanism of protection of individuals with the highest values ​​of the fitness function against accidental elimination. In the classical genetic algorithm, there is a small probability that the most adapted individual will not enter the new population. Therefore, an individual with a maximum value of the fitness function should be protected from accidental elimination. This strategy is called "elite".

There is also a strategy for the transfer of some individuals to a new population without applying genetic operations to them, i.e. parents do not die immediately after the birth of offspring. In addition to this strategy, you can enter the age penalty into the fitness function, i.e. the decrease in its value is proportional to the age of the individual.

Another important modification of the GA is “niche”. In accordance with it, a coefficient is added to the fitness function that is inversely proportional to the number and proximity of neighbors in the multidimensional space of optimized parameters. As a result, the modified fitness function will look like:

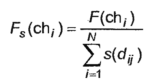(6)


If an individual is alone in his niche, i.e. there are no neighbors like her, the value of the fitness function will not be changed. Otherwise, its value will be reduced in proportion to the proximity and the number of neighbors in the niche. In this case, the degree of proximity can be assessed in various ways.

The introduction of niche allows you to find several extrema, i.e. several optimal models that are close in characteristics to the identified object, but differing from each other.



Conclusion



In conclusion, I would like to say that at present genetic algorithms, along with various modifications, some of which are discussed in this article, and evolutionary strategies are combined under one common name “evolutionary algorithms”. Initially, genetic algorithms and evolutionary strategies developed independently of each other. But later, experts began to combine techniques from these two areas. Currently, the difference between them is not so noticeable. Much of what was stated in the article would be more correctly attributed to evolutionary strategies, but for simplicity of perception it was decided to leave everything as it is.



Thanks for attention! Your comments…



Update 1: at the request of readers, expanding the list of references.



Bibliography



1. Stephan WINKLER, Michael AFFENZELLER, Stefan WAGNER . NEW METHODS FOR THE IDENTIFICATION OF NONLINEAR MODEL STRUCTURES BASED UPON GENETIC PROGRAMMING TECHNIQUES // Institute of Systems Theory and Simulation

2. Rutkovskaya D., Pilinsky M., Rutkovsky L. Neural networks, genetic algorithms and fuzzy systems: Trans. from polish I.D. Rudinsky. - M .: Hotline - Telecom, 2006. - 452 pp., Ill.

3. “Voronoi” turn

4. The criterion of stability of the Routh-Hurwitz

5. State space (control theory)

6. Concepts of the practical use of genetic algorithms

7. “Hello world!” Using genetic algorithms

8. Genetic algorithm

9. Evolutionary algorithms

Source: https://habr.com/ru/post/111075/

More articles:



All Articles