Sort array by O (N) on CUDA
Introduction
Somehow there was a task to sort a unique array of strings using a GPU with a minimum of code and the highest possible speed ...
In this post I will describe the main idea of its solution. As the elements of the sorting array in this post are numbers.
The case with the unique elements of a small array
CUDA was chosen as a platform for reasons that can be considered brand or individual. In fact, there are a lot of examples here at CUDA, and at the moment it has received more development in GPU computing than similar platforms from ATI and OpenCL.
A web search for sorting algorithms on CUDA gave different results. Here is the most interesting . There is a drawing
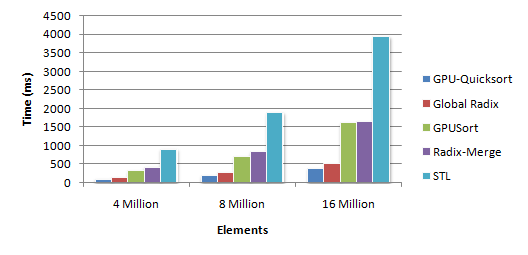
which shows that the best result was given by the QSORT algorithm, which gives the complexity of the order from O (NlogN) to O (N ^ 2). And although parallelization on GPU gave the best result in the article, the doubt crept in that QSORT is not the best way to use the resources of a video card for this task (especially it scared the size of the above code). The following describes the solution of the problem, in fact “one line” with thecomplexity of the time complexity O (N) in the worst case.
So, what we have: modern video cards have more than 500 * 32 streams (GTX275), operating simultaneously, about 15,000.
I had the following conditions for the sorting problem: an array with a length of up to 1000 elements (the general case with a large value is considered further, but I had this). Sorting such an array with O (NlogN) time, with 15,000 threads, seemed somehow wasteful.
As a result of papyrus reasoning, it was found that, in order to achieve the best speed, and this O (N) it is necessary that each thread working simultaneously performs no more than O (N) operations. That is, once passed through our array. And the result of the pass must be a key that determines the position of one element in the resulting sorted array.
Knowing the tid's own thread number (usually from 0..MaxThreads-1), the idea of finding the position of the tid-element as a result was used.
')
Taking the original array as A [] = {1,5,2,4,7}, we assign the task to each thread — find the position of the element A [tid] in the resulting array B [] .
To do this, we set up an auxiliary array K [] - the position of the element A [tid] in the result. ArraySize is the number of elements in A [].
Now thesource code itself is a fragment of the implementation of the proposed algorithm on CUDA \ C (.cu file):
And that's all, the resulting array B [] is sorted by O (N), provided that the number of threads available is greater than or equal to N.
The case with the unique elements of a large array
Now, if we increase the dimension of the array, we can use the same approach, only one thread will look for positions
for [ArraySize / MaxThreads] - (whole part from division) of elements. In this case, the running time of the algorithm will change to [ArraySize / MaxThreads] * O (N), that is, it will increase as many times as the number of array elements is greater than the number of threads available.
For such a case, the implementation of the algorithm will take the form:
Conclusion 1
The promised final sorting algorithm for one stream with number tid, written in one line:
Was: A [i] - unsorted array. Now K [tid] contains indexes of the positions of the original elements in the result. The sorting order is easy to change by choosing between B [K [tid]] = A [tid] and B [ArraySize-K [tid] -1] = A [tid].
Example with data from the beginning
It was: A [] = {1,5,2,4,7}. ArraySize = 5. Run the threads 5.
Flow 0. tid = 0. Set K [tid] = K [0] for A [tid] = A [0] = 1: K [0] = 0
Stream 1. tid = 1. Set K [tid] = K [1] for A [tid] = A [1] = 5: K [1] = 3
Stream 2. tid = 2. A [2] = 2. K [2] = 1
Stream 3. tid = 3. A [3] = 4. K [3] = 2
Stream 4. tid = 4. A [4] = 7. K [4] = 4
Everything. Now, since all the threads were executed at the same time, then we spent time only on enumerating the array - O (N). And got K [] = {0,3,1,2,4}.
Features
When [ArraySize / MaxThreads] issignificantly greater >> ArraySize this algorithm takes complexity greater than O (N ^ 2).
I also do not recommend using it when it is not known in advance whether the elements of the original array are unique.
Conclusions 2
Thus, the original problem was solved for O (N) at worst and O (N) at best (acceleration was only due to N streams of course). And then, provided that the available number of threads is not less than the number of elements of the sorted array.
This post should help novice algorithms researchers to write interesting ideas for fast computations on GPGPU. From the literature I note the book of Kormen algorithms and the portal of interesting problems projecteuler.net.
UPD1. (12/17/2010 13:40)
In the process, it turned out that if the source array A [] takes 16KB of memory, it is still stored and the result of B [] does not work in __shared__ memory (and we use it in CUDA as a level 2 cache to speed up the calculations) - because __shared__ size of only 16KB (for GTX275).
Therefore, the algorithm is supplemented with “parallel swap”, where the result is the original A []:
Now the source array A [] has become sorted using less memory.
UPD2. (12/17/2010 16:34, including )
Faster option due to less access to __shared__ memory and small optimizations.
UPD3 . (12/20/2010 2:16 PM ) I provide the source code for the example: main.cpp , kernel.cu (the dimensions of the array must be within the __shared__ memory of the video card).
UPD4 . (12/23/2010 2:56 PM) Regarding the complexity of O (N): the proposed algorithm is a kind of counting sorting algorithm that has linear time complexity Θ (n + k) © Wiki.
Somehow there was a task to sort a unique array of strings using a GPU with a minimum of code and the highest possible speed ...
In this post I will describe the main idea of its solution. As the elements of the sorting array in this post are numbers.
The case with the unique elements of a small array
CUDA was chosen as a platform for reasons that can be considered brand or individual. In fact, there are a lot of examples here at CUDA, and at the moment it has received more development in GPU computing than similar platforms from ATI and OpenCL.
A web search for sorting algorithms on CUDA gave different results. Here is the most interesting . There is a drawing

which shows that the best result was given by the QSORT algorithm, which gives the complexity of the order from O (NlogN) to O (N ^ 2). And although parallelization on GPU gave the best result in the article, the doubt crept in that QSORT is not the best way to use the resources of a video card for this task (especially it scared the size of the above code). The following describes the solution of the problem, in fact “one line” with the
So, what we have: modern video cards have more than 500 * 32 streams (GTX275), operating simultaneously, about 15,000.
I had the following conditions for the sorting problem: an array with a length of up to 1000 elements (the general case with a large value is considered further, but I had this). Sorting such an array with O (NlogN) time, with 15,000 threads, seemed somehow wasteful.
As a result of papyrus reasoning, it was found that, in order to achieve the best speed, and this O (N) it is necessary that each thread working simultaneously performs no more than O (N) operations. That is, once passed through our array. And the result of the pass must be a key that determines the position of one element in the resulting sorted array.
Knowing the tid's own thread number (usually from 0..MaxThreads-1), the idea of finding the position of the tid-element as a result was used.
')
Taking the original array as A [] = {1,5,2,4,7}, we assign the task to each thread — find the position of the element A [tid] in the resulting array B [] .
To do this, we set up an auxiliary array K [] - the position of the element A [tid] in the result. ArraySize is the number of elements in A [].
Now the
1. MainKernel ( kernel.cu) ArraySize .
MainKernel <<<grids, threads>>> (A,B,ArraySize,MaxThreads);
2. CUDA- MainKernel ( kernel.cu) A[], ArraySize, MaxThreads, B[] K[].
unsigned long tid = blockIdx.x*blockDim.x + threadIdx.x; //
for (unsigned long i = 0;i<ArraySize;++i) // O(N)
if (A[i]<A[tid])
++K[tid]; // O(1)
3. __syncthreads(); //
4. B[K[tid]] = A[tid]; // ( O(1), 3 qsort, swap ..)
* , K[]={0,0,2,3,4}.
.4 , ( O(1)). .And that's all, the resulting array B [] is sorted by O (N), provided that the number of threads available is greater than or equal to N.
The case with the unique elements of a large array
Now, if we increase the dimension of the array, we can use the same approach, only one thread will look for positions
for [ArraySize / MaxThreads] - (whole part from division) of elements. In this case, the running time of the algorithm will change to [ArraySize / MaxThreads] * O (N), that is, it will increase as many times as the number of array elements is greater than the number of threads available.
For such a case, the implementation of the algorithm will take the form:
1. MainKernel ( kernel.cu) [ArraySize/MaxThreads] .
MainKernel <<<grids, threads>>> (A,B,ArraySize,MaxThreads);
2. CUDA- MainKernel ( kernel.cu) A[], ArraySize, MaxThreads, B[] K[].
unsigned long tid = blockIdx.x*blockDim.x + threadIdx.x; //
2.5. , .
unsigned long c = ArraySize/MaxThreads;
for (unsigned long j = 0;j<c;++j) {
unsigned int ttid = c*tid + j; // -
for (unsigned long i = 0;i<ArraySize;++i)
if (A[i]<A[ttid])
++K[ttid]; //
3. __syncthreads(); //
4. B[K[ttid]] = A[ttid]; //
} //Conclusion 1
The promised final sorting algorithm for one stream with number tid, written in one line:
for (unsigned long i = 0;i<ArraySize;++i) if (A[i]<A[tid]) ++K[tid];Was: A [i] - unsorted array. Now K [tid] contains indexes of the positions of the original elements in the result. The sorting order is easy to change by choosing between B [K [tid]] = A [tid] and B [ArraySize-K [tid] -1] = A [tid].
Example with data from the beginning
It was: A [] = {1,5,2,4,7}. ArraySize = 5. Run the threads 5.
Flow 0. tid = 0. Set K [tid] = K [0] for A [tid] = A [0] = 1: K [0] = 0
Stream 1. tid = 1. Set K [tid] = K [1] for A [tid] = A [1] = 5: K [1] = 3
Stream 2. tid = 2. A [2] = 2. K [2] = 1
Stream 3. tid = 3. A [3] = 4. K [3] = 2
Stream 4. tid = 4. A [4] = 7. K [4] = 4
Everything. Now, since all the threads were executed at the same time, then we spent time only on enumerating the array - O (N). And got K [] = {0,3,1,2,4}.
Features
When [ArraySize / MaxThreads] is
I also do not recommend using it when it is not known in advance whether the elements of the original array are unique.
Conclusions 2
Thus, the original problem was solved for O (N) at worst and O (N) at best (acceleration was only due to N streams of course). And then, provided that the available number of threads is not less than the number of elements of the sorted array.
This post should help novice algorithms researchers to write interesting ideas for fast computations on GPGPU. From the literature I note the book of Kormen algorithms and the portal of interesting problems projecteuler.net.
UPD1. (12/17/2010 13:40)
In the process, it turned out that if the source array A [] takes 16KB of memory, it is still stored and the result of B [] does not work in __shared__ memory (and we use it in CUDA as a level 2 cache to speed up the calculations) - because __shared__ size of only 16KB (for GTX275).
Therefore, the algorithm is supplemented with “parallel swap”, where the result is the original A []:
1. for (unsigned long i = 0;i<ArraySize;i++)
if (A[i]<A[tid])
K[tid]++; //
2. __syncthreads(); // !
3. unsigned long B_tid = A[tid]; //, ""
4. __syncthreads(); // ""
5. A[K[tid]] = B_tid; //Now the source array A [] has become sorted using less memory.
UPD2. (12/17/2010 16:34, including )
Faster option due to less access to __shared__ memory and small optimizations.
0. unsigned int K_tid = 0;
1. unsigned long B_tid = A[tid]; //, ""
2. for (unsigned long i = 0;i<ArraySize;++i)
if (A[i]<B_tid)
++K_tid; //
3. __syncthreads(); // ""
4. A[K_tid] = B_tid; //UPD3 . (12/20/2010 2:16 PM ) I provide the source code for the example: main.cpp , kernel.cu (the dimensions of the array must be within the __shared__ memory of the video card).
UPD4 . (12/23/2010 2:56 PM) Regarding the complexity of O (N): the proposed algorithm is a kind of counting sorting algorithm that has linear time complexity Θ (n + k) © Wiki.
Source: https://habr.com/ru/post/110177/
All Articles