Latent semantic analysis
How to find texts similar in meaning? What are the algorithms for searching texts of one subject? - Questions regularly arising on various programmer forums. Today I will talk about one of the approaches that are actively used by search giants and which sounds something like a mantra for SEO aka search engines. This approach calls the latent semantic analysis (LSA), it is also the latent semantic indexing (LSI)

')
Suppose you are faced with the task of writing an algorithm that can distinguish news about pop stars from economic news. The first thing that comes to mind is to select words that are found exclusively in articles of each type and use them for classification. The obvious problem of this approach is: how to list all possible words and what to do in the case when the article contains words from several classes. Additional complexity is represented by homonyms . Those. words with many meanings. For example, the word “banks” in one context may mean glass vessels, and in another context it may be financial institutions.
Latent-semantic analysis displays documents and individual words in the so-called "semantic space", in which all further comparisons are made. The following assumptions are made:
1) Documents are just a bunch of words. The word order in the documents is ignored. It is only important how many times a word occurs in a document.
2) The semantic meaning of a document is defined by a set of words that usually go together. For example, in stock reports, the words “fund”, “share”, “dollar” are often found
3) Each word has a single meaning. This is certainly a strong simplification, but it is this that makes the problem solvable.
For example, I selected several headlines from various news. They were chosen not entirely by chance, the fact is that a random sample would require a very large amount of data, which would make further presentation more difficult. So, several headers have been selected.
First of all, the so-called stop symbols were excluded from these headers. These are words that are found in every text and do not carry a semantic load, these are, first of all, all unions, particles, prepositions and many other words. A complete list of used stop symbols can be found in my previous article on stop-symbols.
Next was the operation of stemming. It is not mandatory, some sources claim that good results are obtained without it. And indeed, if the set of texts is large enough, then this step can be omitted. If the texts are in English, then this step can also be ignored, due to the fact that the number of variations of one or another word form in English is significantly less than in Russian. In our case, you should not skip this step. This will lead to significant degradation of results. For stemming, I used the Porter algorithm .
Further words were found in a single copy. This is also an optional step, it does not affect the final result, but it greatly simplifies mathematical calculations. As a result, we still have the so-called indexed words, they are highlighted in bold:
1. British police know the whereabouts of WikiLeaks founder
2. In the US Court begins the process against the Russians who sent spam.
3. The ceremony of the presentation of the Nobel Prize in the World is boycotted by 19 countries.
4. In the UK, the arrest and founder of the Wikileaks site Julian Assandzh
5. Ukraine ignores the ceremony of presentation of the Nobel Prize
6. The Swedish court refused to consider the founder’s appeal. Wikileaks
7. NATO and the United States have developed plans for the defense of the Baltic countries against Russia
8. UK police found WikiLeaks founder , but did not arrest
9. In Stockholm and Oslo, the Nobel Prize will be presented today.
The first step is to create a frequency matrix of indexed words. In this matrix, the rows correspond to the indexed words, and the columns correspond to the documents. Each cell of the matrix indicates how many times a word occurs in the corresponding document.
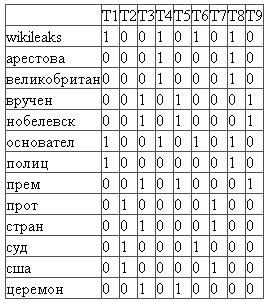
The next step is a singular decomposition of the resulting matrix. Singular decomposition is a mathematical operation decomposing a matrix into three components. Those. We represent the initial matrix M in the form:
M = U * W * V t
where U and V t are orthogonal matrices, and W is a diagonal matrix. Moreover, the diagonal elements of the matrix W are ordered in decreasing order. The diagonal elements of the matrix W are called singular numbers.
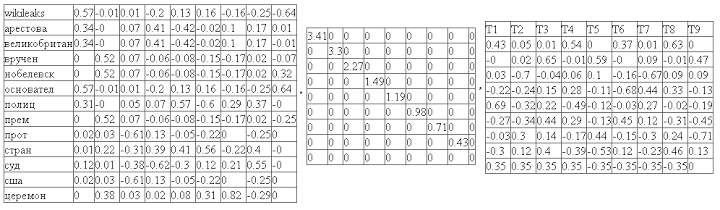
The beauty of singularity decomposition is that it highlights the key components of the matrix, allowing you to ignore noise. According to the simple rules for the product of matrices, it can be seen that the columns and rows corresponding to smaller singular values provide the least contribution to the final product. For example, we can discard the last columns of the matrix U and the last rows of the matrix V ^ t, leaving only the first 2. It is important that this guarantees that the resulting work is optimal. A decomposition of this kind is called a two-dimensional singular decomposition:

Let's now mark on the chart the points corresponding to individual texts and words, we get such an interesting picture:
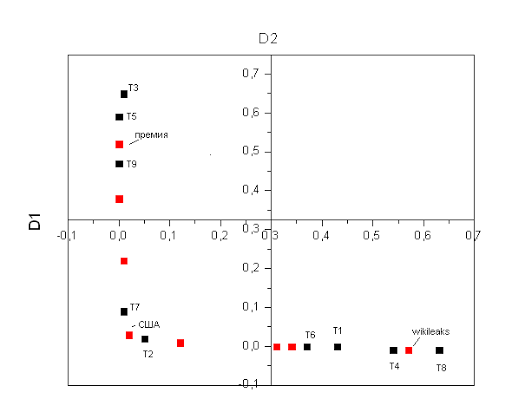
This graph shows that the articles form three independent groups, the first group of articles is located next to the word “wikileaks”, and indeed, if we look at the names of these articles, it becomes clear that they are related to wikileaks. Another group of articles is formed around the word "premium", and indeed there is a discussion of the Nobel Prize.
In practice, of course, the number of groups will be much larger, the space will not be two-dimensional but multi-dimensional, but the idea itself remains the same. We can determine the locations of words and articles in our space and use this information to, for example, determine the subject of the article.
It is easy to see that the overwhelming number of cells in the frequency matrix of indexed words created in the first step contain zeros. The matrix is highly sparse and this property can be used to improve performance and memory consumption when creating a more complex implementation.
In our case, the texts were about the same length, in real situations the frequency matrix should be normalized. The standard way to normalize the matrix TF-IDF
We used two-dimensional decomposition of SVD-2; in real examples, the dimension can be several hundreds or more. The choice of dimension is determined by a specific task, but the general rule is this: the smaller the dimension, the smaller the semantic groups you can find, the greater the dimension, the greater the influence of noise.
For writing the article, a Java library was used to work with Jama matrices . In addition, the SVD function is implemented in well-known math packages like Mathcad, there are libraries for Python and C ++.

')
Suppose you are faced with the task of writing an algorithm that can distinguish news about pop stars from economic news. The first thing that comes to mind is to select words that are found exclusively in articles of each type and use them for classification. The obvious problem of this approach is: how to list all possible words and what to do in the case when the article contains words from several classes. Additional complexity is represented by homonyms . Those. words with many meanings. For example, the word “banks” in one context may mean glass vessels, and in another context it may be financial institutions.
Latent-semantic analysis displays documents and individual words in the so-called "semantic space", in which all further comparisons are made. The following assumptions are made:
1) Documents are just a bunch of words. The word order in the documents is ignored. It is only important how many times a word occurs in a document.
2) The semantic meaning of a document is defined by a set of words that usually go together. For example, in stock reports, the words “fund”, “share”, “dollar” are often found
3) Each word has a single meaning. This is certainly a strong simplification, but it is this that makes the problem solvable.
Example
For example, I selected several headlines from various news. They were chosen not entirely by chance, the fact is that a random sample would require a very large amount of data, which would make further presentation more difficult. So, several headers have been selected.
First of all, the so-called stop symbols were excluded from these headers. These are words that are found in every text and do not carry a semantic load, these are, first of all, all unions, particles, prepositions and many other words. A complete list of used stop symbols can be found in my previous article on stop-symbols.
Next was the operation of stemming. It is not mandatory, some sources claim that good results are obtained without it. And indeed, if the set of texts is large enough, then this step can be omitted. If the texts are in English, then this step can also be ignored, due to the fact that the number of variations of one or another word form in English is significantly less than in Russian. In our case, you should not skip this step. This will lead to significant degradation of results. For stemming, I used the Porter algorithm .
Further words were found in a single copy. This is also an optional step, it does not affect the final result, but it greatly simplifies mathematical calculations. As a result, we still have the so-called indexed words, they are highlighted in bold:
1. British police know the whereabouts of WikiLeaks founder
2. In the US Court begins the process against the Russians who sent spam.
3. The ceremony of the presentation of the Nobel Prize in the World is boycotted by 19 countries.
4. In the UK, the arrest and founder of the Wikileaks site Julian Assandzh
5. Ukraine ignores the ceremony of presentation of the Nobel Prize
6. The Swedish court refused to consider the founder’s appeal. Wikileaks
7. NATO and the United States have developed plans for the defense of the Baltic countries against Russia
8. UK police found WikiLeaks founder , but did not arrest
9. In Stockholm and Oslo, the Nobel Prize will be presented today.
Latent semantic analysis
The first step is to create a frequency matrix of indexed words. In this matrix, the rows correspond to the indexed words, and the columns correspond to the documents. Each cell of the matrix indicates how many times a word occurs in the corresponding document.

The next step is a singular decomposition of the resulting matrix. Singular decomposition is a mathematical operation decomposing a matrix into three components. Those. We represent the initial matrix M in the form:
M = U * W * V t
where U and V t are orthogonal matrices, and W is a diagonal matrix. Moreover, the diagonal elements of the matrix W are ordered in decreasing order. The diagonal elements of the matrix W are called singular numbers.

The beauty of singularity decomposition is that it highlights the key components of the matrix, allowing you to ignore noise. According to the simple rules for the product of matrices, it can be seen that the columns and rows corresponding to smaller singular values provide the least contribution to the final product. For example, we can discard the last columns of the matrix U and the last rows of the matrix V ^ t, leaving only the first 2. It is important that this guarantees that the resulting work is optimal. A decomposition of this kind is called a two-dimensional singular decomposition:

Let's now mark on the chart the points corresponding to individual texts and words, we get such an interesting picture:

This graph shows that the articles form three independent groups, the first group of articles is located next to the word “wikileaks”, and indeed, if we look at the names of these articles, it becomes clear that they are related to wikileaks. Another group of articles is formed around the word "premium", and indeed there is a discussion of the Nobel Prize.
In practice, of course, the number of groups will be much larger, the space will not be two-dimensional but multi-dimensional, but the idea itself remains the same. We can determine the locations of words and articles in our space and use this information to, for example, determine the subject of the article.
Algorithm improvements
It is easy to see that the overwhelming number of cells in the frequency matrix of indexed words created in the first step contain zeros. The matrix is highly sparse and this property can be used to improve performance and memory consumption when creating a more complex implementation.
In our case, the texts were about the same length, in real situations the frequency matrix should be normalized. The standard way to normalize the matrix TF-IDF
We used two-dimensional decomposition of SVD-2; in real examples, the dimension can be several hundreds or more. The choice of dimension is determined by a specific task, but the general rule is this: the smaller the dimension, the smaller the semantic groups you can find, the greater the dimension, the greater the influence of noise.
Remarks
For writing the article, a Java library was used to work with Jama matrices . In addition, the SVD function is implemented in well-known math packages like Mathcad, there are libraries for Python and C ++.
Source: https://habr.com/ru/post/110078/
All Articles