Search for faces based on hidden Markov models
At the moment, there is an avalanche increase in the number of multimedia resources, in particular images. As a result, the requirements for the means of organizing and searching for such resources are increasing. Most of the currently existing systems
carrying out the search for information on the description (English Description-Based Image Retrieval, DBIR), can no longer fully meet human needs. Therefore, an increasing interest in searching for objects in content (English Content-Based Image Retrieval, CBIR).
It should be noted that in many areas of the user has to deal with images of human faces: from the rapidly developing social networks and ending with the field of forensics. And although the general methods of search and classification are applicable to this task, it requires a higher accuracy of the solution. Such a requirement is explained, by and large, by the complexity of the structure of the face itself and the many details that make it difficult to identify common types of faces (moles, hairstyles, facial hair, etc.). It is quite natural that the requirement for accuracy of the result leads to an increase in the computational costs of search and face recognition algorithms.
There are quite a number of methods that allow you to process images of individuals: the method of own faces, neural networks, etc. Among them are algorithms based on hidden Markov models. This method shows one of the highest results in the tasks of facial recognition.
Before proceeding to the consideration of models, consider what constitutes a Markov chain (Markov process). A sequence of random variables X n is called a Markov chain if:
P (X n = a | X n-1 = b, X n-2 = c, ..., X 0 = x) = P (X n | X = b) .
It is proved that Markov chains allow you to create fairly simple and informative pictures. You can, for example, draw a weighted directed graph with a node for each state and a weighting factor on each edge indicating the probability of transition between states:
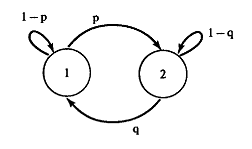
When observing a random variable X n, it is known what state the chain is in. This model, unfortunately, is too limited and it is not able to solve many actual problems. A more perfect model can be obtained by assuming that for each element of the sequence there is a different random variable, the probability distribution of which depends on the state of the chain - there is some variable Y n , and the probability distribution at some point P (Y n | X n = s i ) = q i (Y n ) . These elements can be collected in the matrix Q. Models of this kind are called hidden Markov models (SMM) . To specify the SMM, it is required to provide a transition between states, a relationship between a state and a probability distribution.
Y n , and also know the initial distribution of states.
')
Consider the formal description of the hidden Markov model. Each model is determined by the following parameters:
Each element of a nested SMM is called a superstate and is a separate one-dimensional Markov model with the parameters described above.
The digital image is the essence of a random two-dimensional discrete signal observed by the system. The sequence of observations (vector of observations) can be extracted from the image in various ways. Because of this, the descriptive abilities of the models obtained may vary. Most preferred is the option to scan an image with a rectangular window. To reduce the likelihood of data loss at the block boundaries, it is recommended to scan the image so that adjacent blocks of pixels can overlap each other. The value of the overlap is chosen experimentally.
To reduce computational complexity and reduce the space of attributes, each extracted block of pixels undergoes some transformation, which results in a certain set of numerical data, which is the vector of observations.
The most suitable for the task are two transformations:
Further, the obtained vectors are distributed over the states of the model. It should be noted here that each individual SMM represents a certain class of objects. Then the state of the model determines some key features of the class. For example, the SMM for face search consists of 5 superstates corresponding to the face areas (frontal part, eyes, nose, mouth, chin), each of which is divided into separate states.
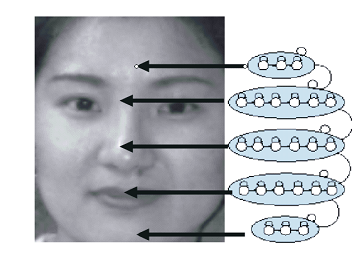
The transition to the next state is possible only after the previous one, and the transition to the next super-state is possible only after all the states of the current super-state. The probability that a certain object belongs to a given class is estimated as the probability of generating a signal corresponding to its feature vector.
We assume that information about the images of the collection is stored in a relational database. Image content can be defined at various levels of abstraction. At the lowest level, an image is a collection of pixels. The pixel level is rarely used in a search task, since it implies large computational and time costs.
Raw data can be sent to generate numeric descriptors that describe particular visual characteristics, called signatures . As a rule, the level of image signatures requires much less space than the image.
Image search is based on the search for similarity in multidimensional space. The image is determined by a set of their signatures. The similarity measure is a function that calculates and returns a value corresponding to the similarity between two objects according to some predefined criteria. The concept of measure of similarity is based on the concept of a metric . A metric is a function of distance d , defined on a metric set, for any x, y points whose z
the conditions are met:
one. ,
,
2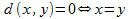 ,
,
3 .
.
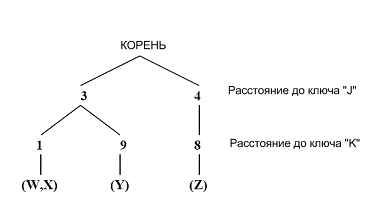
Indexing and searching of images in collections is performed on the basis of a triangular tree (triangle tree, trie tree), also called Really Fixed Query Tree. A triangle tree is a data structure designed to find approximate matches based on search efforts. It is associated with a measure of distance, a set of key images and a set of database elements. The trie form is a tree form in which the edges follow from root to leaf, defining the leaf index. The leaves of the tree contain elements of the base. Each internal edge in the tree is associated with a non-negative number. Each level of the tree is associated with a single key. The path from the root to the leaves is the distance from the database item to each of the keys.
The figure shows a triangular tree with 4 elements ( W , X , Y , Z) and 2 keys ( J , K ). The distance from the sheet W to the key J is 3, the distance from W to K is 1. Thus, each image will be characterized by a certain set of numerical values, defined as the distance from this image to the existing keys.
The process of indexing the collection of images consists in finding the distances from each image to each key. Based on the foregoing, the search principle can be defined as follows. Let I represent the base object, Q represent the query object, K represent the key images, and d define some similarity measures — metrics. Using the property of metric (3), we conclude that the following inequalities will be true:

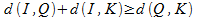
Combining inequalities, we get an expression that determines the distance from the request object to the collection object:
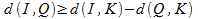
Thus, by comparing objects from a database and objects of a query with a third key object, the lower limit of the distance between two objects can be obtained. Based on this boundary, most of the collection can be cut off as not satisfying the request.
It should also be noted that the search process takes place in two stages. At the first stage, the lower limit of the distance from the request image to the collection images is determined. At this stage, part of the collection is cut off. At the second stage, a refinement search takes place: the distances from the request image to each image are determined, from those found at the first stage. Images corresponding to maximum distances make up the final search result.
Based on the above, we can conclude that in order to use search and indexing, you must be able to perform the following actions for each image.
The second problem is that at this stage it is not possible to use the SMM to find the distance between two separate images. This is due to the fact that search algorithms require a trained model: teaching a model on one image is problematic.
The following materials were used in the preparation of the article:
carrying out the search for information on the description (English Description-Based Image Retrieval, DBIR), can no longer fully meet human needs. Therefore, an increasing interest in searching for objects in content (English Content-Based Image Retrieval, CBIR).
It should be noted that in many areas of the user has to deal with images of human faces: from the rapidly developing social networks and ending with the field of forensics. And although the general methods of search and classification are applicable to this task, it requires a higher accuracy of the solution. Such a requirement is explained, by and large, by the complexity of the structure of the face itself and the many details that make it difficult to identify common types of faces (moles, hairstyles, facial hair, etc.). It is quite natural that the requirement for accuracy of the result leads to an increase in the computational costs of search and face recognition algorithms.
There are quite a number of methods that allow you to process images of individuals: the method of own faces, neural networks, etc. Among them are algorithms based on hidden Markov models. This method shows one of the highest results in the tasks of facial recognition.
Hidden Markov Models
Before proceeding to the consideration of models, consider what constitutes a Markov chain (Markov process). A sequence of random variables X n is called a Markov chain if:
P (X n = a | X n-1 = b, X n-2 = c, ..., X 0 = x) = P (X n | X = b) .
It is proved that Markov chains allow you to create fairly simple and informative pictures. You can, for example, draw a weighted directed graph with a node for each state and a weighting factor on each edge indicating the probability of transition between states:

When observing a random variable X n, it is known what state the chain is in. This model, unfortunately, is too limited and it is not able to solve many actual problems. A more perfect model can be obtained by assuming that for each element of the sequence there is a different random variable, the probability distribution of which depends on the state of the chain - there is some variable Y n , and the probability distribution at some point P (Y n | X n = s i ) = q i (Y n ) . These elements can be collected in the matrix Q. Models of this kind are called hidden Markov models (SMM) . To specify the SMM, it is required to provide a transition between states, a relationship between a state and a probability distribution.
Y n , and also know the initial distribution of states.
')
Consider the formal description of the hidden Markov model. Each model is determined by the following parameters:
- The set S = {s 1 , s 2 , ..., s N } of N states.
- The initial probability distribution is P = {p i } .
- Matrix of transition probabilities between states A = {a i } .
- The matrix of the probability of generating observations is B = {b j (O t ) } , where b j (O t ) is the probability of generating the observation O t at the moment of time t in the state q t = s j , b j (O t ) = P (O t | q t = s j ) .
Each element of a nested SMM is called a superstate and is a separate one-dimensional Markov model with the parameters described above.
Image in terms of recognition
The digital image is the essence of a random two-dimensional discrete signal observed by the system. The sequence of observations (vector of observations) can be extracted from the image in various ways. Because of this, the descriptive abilities of the models obtained may vary. Most preferred is the option to scan an image with a rectangular window. To reduce the likelihood of data loss at the block boundaries, it is recommended to scan the image so that adjacent blocks of pixels can overlap each other. The value of the overlap is chosen experimentally.
To reduce computational complexity and reduce the space of attributes, each extracted block of pixels undergoes some transformation, which results in a certain set of numerical data, which is the vector of observations.
The most suitable for the task are two transformations:
- Karunen-Loeve transform (eng. Karhunen-Loeve transform - abbr. KLT);
- discrete cosine transform (English Discrete Cosine
Transform - abbr. DCT).
Further, the obtained vectors are distributed over the states of the model. It should be noted here that each individual SMM represents a certain class of objects. Then the state of the model determines some key features of the class. For example, the SMM for face search consists of 5 superstates corresponding to the face areas (frontal part, eyes, nose, mouth, chin), each of which is divided into separate states.

The transition to the next state is possible only after the previous one, and the transition to the next super-state is possible only after all the states of the current super-state. The probability that a certain object belongs to a given class is estimated as the probability of generating a signal corresponding to its feature vector.
Face search
We assume that information about the images of the collection is stored in a relational database. Image content can be defined at various levels of abstraction. At the lowest level, an image is a collection of pixels. The pixel level is rarely used in a search task, since it implies large computational and time costs.
Raw data can be sent to generate numeric descriptors that describe particular visual characteristics, called signatures . As a rule, the level of image signatures requires much less space than the image.
Image search is based on the search for similarity in multidimensional space. The image is determined by a set of their signatures. The similarity measure is a function that calculates and returns a value corresponding to the similarity between two objects according to some predefined criteria. The concept of measure of similarity is based on the concept of a metric . A metric is a function of distance d , defined on a metric set, for any x, y points whose z
the conditions are met:
one.
 ,
,2
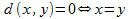 ,
,3
 .
.Indexing and searching of images in collections is performed on the basis of a triangular tree (triangle tree, trie tree), also called Really Fixed Query Tree. A triangle tree is a data structure designed to find approximate matches based on search efforts. It is associated with a measure of distance, a set of key images and a set of database elements. The trie form is a tree form in which the edges follow from root to leaf, defining the leaf index. The leaves of the tree contain elements of the base. Each internal edge in the tree is associated with a non-negative number. Each level of the tree is associated with a single key. The path from the root to the leaves is the distance from the database item to each of the keys.
The figure shows a triangular tree with 4 elements ( W , X , Y , Z) and 2 keys ( J , K ). The distance from the sheet W to the key J is 3, the distance from W to K is 1. Thus, each image will be characterized by a certain set of numerical values, defined as the distance from this image to the existing keys.

The process of indexing the collection of images consists in finding the distances from each image to each key. Based on the foregoing, the search principle can be defined as follows. Let I represent the base object, Q represent the query object, K represent the key images, and d define some similarity measures — metrics. Using the property of metric (3), we conclude that the following inequalities will be true:

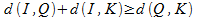
Combining inequalities, we get an expression that determines the distance from the request object to the collection object:
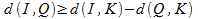
Thus, by comparing objects from a database and objects of a query with a third key object, the lower limit of the distance between two objects can be obtained. Based on this boundary, most of the collection can be cut off as not satisfying the request.
It should also be noted that the search process takes place in two stages. At the first stage, the lower limit of the distance from the request image to the collection images is determined. At this stage, part of the collection is cut off. At the second stage, a refinement search takes place: the distances from the request image to each image are determined, from those found at the first stage. Images corresponding to maximum distances make up the final search result.
Based on the above, we can conclude that in order to use search and indexing, you must be able to perform the following actions for each image.
- Highlight image signatures. For single images, the signature will be the observation vectors of each face contained on it.
- Highlight key signatures. In this case, for the search system based on the SMM, the keys will be sets of images of one person, and the signature will be the parameters of the model trained on these images.
- Compare key signatures and images, as well as two images. The result of the comparison should be the distance, expressed as an integer, lying in the segment [0; 99].
The second problem is that at this stage it is not possible to use the SMM to find the distance between two separate images. This is due to the fact that search algorithms require a trained model: teaching a model on one image is problematic.
The following materials were used in the preparation of the article:
- Nefian, AV Hidden Markov Madel-Based Approach for Face Detection and Recognition / Ara Nefian. 1999
- Josan, O.V. Using Hidden Markov Models for Detecting Iris on Faces: 2006 / A.V. Jozan, Moscow State University Lomonosov. - 2006.
- Gultyaeva, T.A. Hidden Markov models with one-dimensional topology in the problem of face recognition / TA Gultyaev, A.A. Popov; NSTU. - 2006.
- Berman, AP A Flexible Image Database System for Content-Based Retrieval: Computer Vision and Understanding / AP Berman, LG Shapiro. 1999
Source: https://habr.com/ru/post/109956/
All Articles