Pulling out Direct from all information about competitors campaigns
In continuation of the article by Evgeny Cheskidov “Yandex. Direct. Analyzing the competitive environment ” I want to show how, using not very complicated calculations and the Yandex API, to pull literally all the information about competitors' advertising campaigns from Yandex.Direct. I’ll say right away that the idea hasn’t been tested in practice yet, the very fact of having all the information and, accordingly, the possibility of this calculation was shown by Cheskidov only yesterday, and the algorithm was born literally now. But mathematically everything seems to fit. Carefully, under the cut a lot of formulas.
i is the ordinal number of the ad on the "show all advertising results" page.
b [i] = bid, while the unknown maximum bid for the i-th ad. It follows from the rules of Yandex.Direct that
20 ≥ b [1] ≥ b [2] ≥ b [3] ≥… ≥ b [i] ≥ b [i + 1] ≥… ≥ 0.01 (1)
c [i] - while unknown to us CTR of the i-th announcement, 0.01 ≤ c [i] ≤ 1.0
')
a [i] is the “effective bid” by which ads in the SERP are sorted, by definition
a [i] = b [i] ∙ c [i] (2)
o [i] - position of the i-th announcement in the SERP (search results page). The order in the SERP is determined by a, and not by b, therefore, in the general case, o [i] ≠ i. This fact is discussed in detail in the article by Cheskidov.
r [j] - is the inverse function to o [i], that is, r [o [i]] = o [r [i]] = i. Physically, this is the ad index i, which occupies the j-th position in the SERP, if we assume that there are ads with numbers j = 1 ... 3 in the special placement, and in the right-hand block - with numbers j = 4 ... 10.
From the rules of the competition of the Directive in issuing SERPa, we know that
a [r [1]] ≥ a [r [2]] ≥… ≥ a [r [j]] ≥ a [r [j + 1]] ≥… (3)
s [i] is the number of impressions strategy for close key phrases selected for the i-th ad:
• s [i] = 0, if the phrase without quotes and negative keywords is used as the key phrase
• s [i] = 1 if the keyword phrase with negative keywords is used
• s [i] = 2, if you use the keyword phrase in quotes
The case s [i] = 2 can be determined by noting the absence of an ad for a key phrase with a non-existent word, for example, [pink elephants fv243ae]. To determine the case of s [i] = 1, you need to find in the WordState the most obvious (frequency) negative keyword for the query and check the availability of an ad on request with this negative word, for example [pink elephants free].
For the “budget forecast” for each strategy s, one can pull out the averaged values of the initial conditions b0, c0 and, accordingly, a0:
b0 [s, 1] - forecast of the price of the first place in the special placement
b0 [s, 3] - forecast for the price of entry to the special placement
c0 [s, 3] - CTR forecast in special placement
b0 [s, 4] - first place price forecast
c0 [s, 4] - first place CTR forecast
b0 [s, 10] - forecast of the entrance price to guaranteed impressions
c0 [s, 10] - CTR forecast in guaranteed impressions.
Once again, we note that these are averaged forecasts, and not real values of parameters, that is,
b0 [s, i] ≠ b [i] for all i> 1
But it can be argued that the effective rate a [i] in the forecast is exactly equal to the real effective rate of the i-th place, i.e.
a0 [s [i], i] = a [r [i]], and more specifically
a0 [s [3], 3] = a [r [3]] (4)
a0 [s [4], 4] = a [r [4]] (5)
a0 [s [10], 10] = a [r [10]] (6)
Finally, let us denote by K [s] the total number of requests per month for the key phrase for each strategy.
How does a person view a results page? Reads the first ad, with some probability p clicks on it, otherwise reads the second ad, again with some probability clicks, and so on. We translate this into the language of formulas and denote by Xi a discrete event equal to 1 if the user clicked on the i-th declaration, and 0 if not clicked:

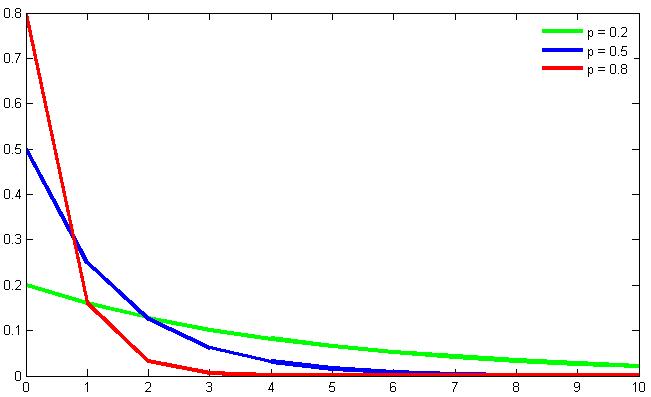
Since the SERP is viewed by thousands of users, such events are independent. Mathematicians have proved that in such a model, the probability of a click on the i-th position obeys the law of geometric distribution and is equal to
P (n) = p ∙ (1-p) n , (7)
where n is the number of the announcement, starting from zero, and p is a certain parameter depending on the specific keyword phrase.
By itself, the P (n) function is not yet a CTR, since it only takes into account the position of the ad on the page. In Direct, the CTR is also affected by the sample for which a particular ad is shown (that is, the impression strategy), the position history (accumulated CTR), and the quality of the ad itself. History can be gained by systematically scanning the SERP. As for the quality of the ads themselves, in competitive topics it is about the same, and, as users do not read the output, and view it diagonally, it does not play a big role.
Translating from mathematical to Russian, an ad for the 8th position cannot have a CTR of 70% or at least 20%. And vice versa, you, of course, can place a disgusting advertisement in the first place of special placement and “crush money”, but whatever your budget, as the statistics from the CTR users of this ad fall, you will inevitably fall first from the first place, and then generally from the shows.
So in this article, for simplicity, I will consider the CTR as a function of position and strategy. Interested readers can take into account such factors as the history of a change in positions, the occurrence of a key phrase in the ad text, or the relevance of the ad text to the other ads on the page.
It should be noted that there is still a slight fatal discrepancy between theory and practice: in mathematics, the sequence is assumed to be infinite, and the actual output is limited. This leads to the fact that the actual CTR of the most recent announcements in the block is slightly overestimated relative to the theoretical probability.
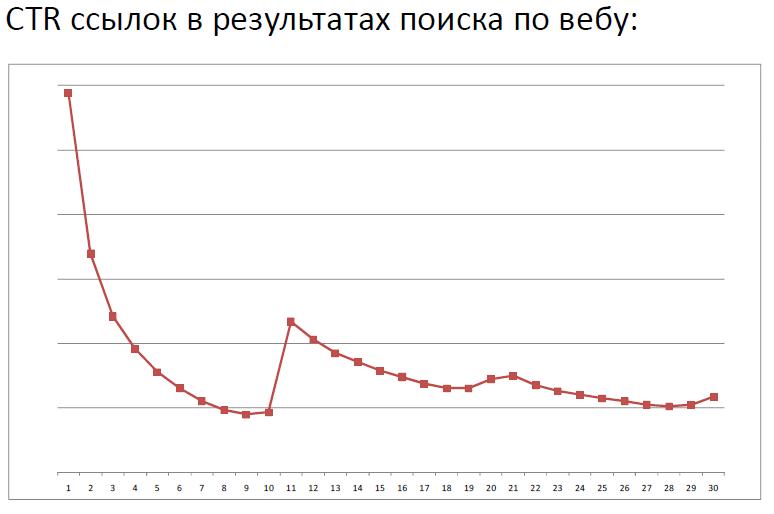
To make it at least a little clear what was discussed in the previous paragraphs, here are two graphs:
The first one shows a graph of CTR dependence on the position from the report by Alexander Sadovsky :
The second graph shows the probability function for the geometric distribution with different parameters p (from Wikipedia)
Knowing for each ad its position and strategy, we need to estimate the expected CTR of this ad, that is, calculate the parameter p from formula (7).
For the right block, everything is simple, the expected CTR of the first place in the right block is given to us by Yandex, that is,
pr [s] = c0 [s, 4] (8)
which must be calculated for all strategies s.
Knowing pr, we can calculate theoretical values of c1 for all i using the formula
c1 [s, r [i]] = pr [s] ∙ (1 - pr [s]) r [i] -4 (9)
For the upper block (there is another parameter p), everything is a bit more complicated, since Yandex does not disclose the CTR value for the third ad, not for the first announcement in special allocation. We'll have to look for a math reference book and solve a cubic equation
p 3 - 2p 2 + p - c0 [s, 3] = 0 (10)
Further, similar to (8), only the exponent will be r [i] -1.
We write out expressions (1) and (3) in the form of a system of ordinary inequalities
b [1] ≥ b [2]
b [2] ≥ b [3]
...
b [9] ≥ b [10]
b [r [1]] ∙ with [r [1]] ≥ b [r [2]] ∙ c [r [2]]
b [r [2]] ∙ with [r [2]] ≥ b [r [3]] ∙ c [r [3]]
...
b [r [9]] ∙ with [r [9]] ≥ b [r [9]] ∙ c [r [9]]
(for the case with N = 10 ads)
Note: we will not be able to solve the system, if there are more than 10 ads - we simply will not see the “second page of direct” and will not know the relationship between a [r [i]] for i> 10. Ads-outsiders will have to throw out the calculations.
Add to the system the boundary conditions on b and c and the initial values given by equations (4) ... (6).
Thus, we obtain a system of second-order inequalities with 2N unknowns, 3N inequalities, and three equations. The property of this system is such that for each pair of unknowns b [i], c [i] there is a small hyperbolic region in which these parameters can change without violating the conditions of inequalities.
To resolve this uncertainty, we need to add additional restrictions on b and c in such a way that b [i] tend to zero while maintaining positions (no one will overpay just like that), and c [i] tend to theoretically expected values.
With these additional restrictions, we will not be able to find the real value of the maximum bids, but only the minimum required values for the ads to take their place. In practice, this means that if the most expensive ad has a bid of $ 10, but in reality for the first place you need only $ 3.01, we will find the value of 3.01. But in our case it does not matter, because Yandex already tells us the highest bid for a keyword, and all other bets are consistently lower than the previous one.
We introduce a “penalty function” into the system — a measure indicating how far the approximate solution does not satisfy our conditions.
The structure of the penalty function will be something like this:
1. A large penalty for failure to comply with inequalities (1) (ordering b [i]), a small penalty for over-fulfilling these inequalities;
2. Large penalty for failure to comply with inequalities (2) (ordering a [i]), zero penalty for their implementation.
3. A very large penalty for non-compliance with the boundary conditions on c [i]
4. A large penalty for non-compliance with equations (4) ... (6).
5. Some penalty for deviation of c [i] -th from theoretical values.
Thus, we obtain the usual problem of optimizing the penalty function, that is, searching for such values of b [i] and c [i], for which the value of the penalty function will be minimal. Algorithms for finding such a solution have long been known from the section of mathematics, which is called “optimization methods”. Applying the appropriate algorithm, we will eventually get the values of b [i] and c [i], that is, the rates and CTR for all competing ads.
Now the most interesting thing: knowing for each ad the rate, CTR, strategy and number of impressions K [s], we can estimate the maximum monthly budget of each ad for this keyword. Knowing CTR and K [s] - estimate the number of conversions and, thus, the targeted traffic on the competitor's site. And knowing the budget and the number of transitions, we can estimate the cost of each transition, that is, the quality of setting up an advertising campaign. Knowing the quality of the advertising campaign, we can make far-reaching conclusions, which, however, are no longer described by any mathematics)
Finally, knowing the semantic core of the domain and connecting to the direct via the API, we can calculate the total budget of all advertising campaigns of competitors across the core in almost automatic mode. “Almost” - because the core and negative keywords will still have to be manually selected.
And knowing the real budgets of all competitors ... well, you understand.
In general, Yandex provided all the information to play with open eyes.
Here is such an applied Data Mining in action.
1. To begin with, we introduce the notation:
i is the ordinal number of the ad on the "show all advertising results" page.
b [i] = bid, while the unknown maximum bid for the i-th ad. It follows from the rules of Yandex.Direct that
20 ≥ b [1] ≥ b [2] ≥ b [3] ≥… ≥ b [i] ≥ b [i + 1] ≥… ≥ 0.01 (1)
c [i] - while unknown to us CTR of the i-th announcement, 0.01 ≤ c [i] ≤ 1.0
')
a [i] is the “effective bid” by which ads in the SERP are sorted, by definition
a [i] = b [i] ∙ c [i] (2)
o [i] - position of the i-th announcement in the SERP (search results page). The order in the SERP is determined by a, and not by b, therefore, in the general case, o [i] ≠ i. This fact is discussed in detail in the article by Cheskidov.
r [j] - is the inverse function to o [i], that is, r [o [i]] = o [r [i]] = i. Physically, this is the ad index i, which occupies the j-th position in the SERP, if we assume that there are ads with numbers j = 1 ... 3 in the special placement, and in the right-hand block - with numbers j = 4 ... 10.
From the rules of the competition of the Directive in issuing SERPa, we know that
a [r [1]] ≥ a [r [2]] ≥… ≥ a [r [j]] ≥ a [r [j + 1]] ≥… (3)
s [i] is the number of impressions strategy for close key phrases selected for the i-th ad:
• s [i] = 0, if the phrase without quotes and negative keywords is used as the key phrase
• s [i] = 1 if the keyword phrase with negative keywords is used
• s [i] = 2, if you use the keyword phrase in quotes
The case s [i] = 2 can be determined by noting the absence of an ad for a key phrase with a non-existent word, for example, [pink elephants fv243ae]. To determine the case of s [i] = 1, you need to find in the WordState the most obvious (frequency) negative keyword for the query and check the availability of an ad on request with this negative word, for example [pink elephants free].
For the “budget forecast” for each strategy s, one can pull out the averaged values of the initial conditions b0, c0 and, accordingly, a0:
b0 [s, 1] - forecast of the price of the first place in the special placement
b0 [s, 3] - forecast for the price of entry to the special placement
c0 [s, 3] - CTR forecast in special placement
b0 [s, 4] - first place price forecast
c0 [s, 4] - first place CTR forecast
b0 [s, 10] - forecast of the entrance price to guaranteed impressions
c0 [s, 10] - CTR forecast in guaranteed impressions.
Once again, we note that these are averaged forecasts, and not real values of parameters, that is,
b0 [s, i] ≠ b [i] for all i> 1
But it can be argued that the effective rate a [i] in the forecast is exactly equal to the real effective rate of the i-th place, i.e.
a0 [s [i], i] = a [r [i]], and more specifically
a0 [s [3], 3] = a [r [3]] (4)
a0 [s [4], 4] = a [r [4]] (5)
a0 [s [10], 10] = a [r [10]] (6)
Finally, let us denote by K [s] the total number of requests per month for the key phrase for each strategy.
2. The statistical model of the user Yandex
How does a person view a results page? Reads the first ad, with some probability p clicks on it, otherwise reads the second ad, again with some probability clicks, and so on. We translate this into the language of formulas and denote by Xi a discrete event equal to 1 if the user clicked on the i-th declaration, and 0 if not clicked:

Since the SERP is viewed by thousands of users, such events are independent. Mathematicians have proved that in such a model, the probability of a click on the i-th position obeys the law of geometric distribution and is equal to
P (n) = p ∙ (1-p) n , (7)
where n is the number of the announcement, starting from zero, and p is a certain parameter depending on the specific keyword phrase.
By itself, the P (n) function is not yet a CTR, since it only takes into account the position of the ad on the page. In Direct, the CTR is also affected by the sample for which a particular ad is shown (that is, the impression strategy), the position history (accumulated CTR), and the quality of the ad itself. History can be gained by systematically scanning the SERP. As for the quality of the ads themselves, in competitive topics it is about the same, and, as users do not read the output, and view it diagonally, it does not play a big role.
Translating from mathematical to Russian, an ad for the 8th position cannot have a CTR of 70% or at least 20%. And vice versa, you, of course, can place a disgusting advertisement in the first place of special placement and “crush money”, but whatever your budget, as the statistics from the CTR users of this ad fall, you will inevitably fall first from the first place, and then generally from the shows.
So in this article, for simplicity, I will consider the CTR as a function of position and strategy. Interested readers can take into account such factors as the history of a change in positions, the occurrence of a key phrase in the ad text, or the relevance of the ad text to the other ads on the page.
It should be noted that there is still a slight fatal discrepancy between theory and practice: in mathematics, the sequence is assumed to be infinite, and the actual output is limited. This leads to the fact that the actual CTR of the most recent announcements in the block is slightly overestimated relative to the theoretical probability.
To make it at least a little clear what was discussed in the previous paragraphs, here are two graphs:
The first one shows a graph of CTR dependence on the position from the report by Alexander Sadovsky :

The second graph shows the probability function for the geometric distribution with different parameters p (from Wikipedia)

3. Calculation of theoretical CTR
Knowing for each ad its position and strategy, we need to estimate the expected CTR of this ad, that is, calculate the parameter p from formula (7).
For the right block, everything is simple, the expected CTR of the first place in the right block is given to us by Yandex, that is,
pr [s] = c0 [s, 4] (8)
which must be calculated for all strategies s.
Knowing pr, we can calculate theoretical values of c1 for all i using the formula
c1 [s, r [i]] = pr [s] ∙ (1 - pr [s]) r [i] -4 (9)
For the upper block (there is another parameter p), everything is a bit more complicated, since Yandex does not disclose the CTR value for the third ad, not for the first announcement in special allocation. We'll have to look for a math reference book and solve a cubic equation
p 3 - 2p 2 + p - c0 [s, 3] = 0 (10)
Further, similar to (8), only the exponent will be r [i] -1.
4. Putting the system of equations.
We write out expressions (1) and (3) in the form of a system of ordinary inequalities
b [1] ≥ b [2]
b [2] ≥ b [3]
...
b [9] ≥ b [10]
b [r [1]] ∙ with [r [1]] ≥ b [r [2]] ∙ c [r [2]]
b [r [2]] ∙ with [r [2]] ≥ b [r [3]] ∙ c [r [3]]
...
b [r [9]] ∙ with [r [9]] ≥ b [r [9]] ∙ c [r [9]]
(for the case with N = 10 ads)
Note: we will not be able to solve the system, if there are more than 10 ads - we simply will not see the “second page of direct” and will not know the relationship between a [r [i]] for i> 10. Ads-outsiders will have to throw out the calculations.
Add to the system the boundary conditions on b and c and the initial values given by equations (4) ... (6).
Thus, we obtain a system of second-order inequalities with 2N unknowns, 3N inequalities, and three equations. The property of this system is such that for each pair of unknowns b [i], c [i] there is a small hyperbolic region in which these parameters can change without violating the conditions of inequalities.
To resolve this uncertainty, we need to add additional restrictions on b and c in such a way that b [i] tend to zero while maintaining positions (no one will overpay just like that), and c [i] tend to theoretically expected values.
With these additional restrictions, we will not be able to find the real value of the maximum bids, but only the minimum required values for the ads to take their place. In practice, this means that if the most expensive ad has a bid of $ 10, but in reality for the first place you need only $ 3.01, we will find the value of 3.01. But in our case it does not matter, because Yandex already tells us the highest bid for a keyword, and all other bets are consistently lower than the previous one.
We introduce a “penalty function” into the system — a measure indicating how far the approximate solution does not satisfy our conditions.
The structure of the penalty function will be something like this:
1. A large penalty for failure to comply with inequalities (1) (ordering b [i]), a small penalty for over-fulfilling these inequalities;
2. Large penalty for failure to comply with inequalities (2) (ordering a [i]), zero penalty for their implementation.
3. A very large penalty for non-compliance with the boundary conditions on c [i]
4. A large penalty for non-compliance with equations (4) ... (6).
5. Some penalty for deviation of c [i] -th from theoretical values.
Thus, we obtain the usual problem of optimizing the penalty function, that is, searching for such values of b [i] and c [i], for which the value of the penalty function will be minimal. Algorithms for finding such a solution have long been known from the section of mathematics, which is called “optimization methods”. Applying the appropriate algorithm, we will eventually get the values of b [i] and c [i], that is, the rates and CTR for all competing ads.
5. PROFIT!
Now the most interesting thing: knowing for each ad the rate, CTR, strategy and number of impressions K [s], we can estimate the maximum monthly budget of each ad for this keyword. Knowing CTR and K [s] - estimate the number of conversions and, thus, the targeted traffic on the competitor's site. And knowing the budget and the number of transitions, we can estimate the cost of each transition, that is, the quality of setting up an advertising campaign. Knowing the quality of the advertising campaign, we can make far-reaching conclusions, which, however, are no longer described by any mathematics)
Finally, knowing the semantic core of the domain and connecting to the direct via the API, we can calculate the total budget of all advertising campaigns of competitors across the core in almost automatic mode. “Almost” - because the core and negative keywords will still have to be manually selected.
And knowing the real budgets of all competitors ... well, you understand.
In general, Yandex provided all the information to play with open eyes.
Here is such an applied Data Mining in action.
Source: https://habr.com/ru/post/107898/
All Articles