“Live graphs” - growing graphs on cellular automata with Silverlight examples

Introduction

Perhaps nothing for so long, for centuries, did not interest scientists, as questions about the origin of life and mind. How did nature guess to create the human brain? What determines the structure of the neural network in our head and how does the autoassembly of a multicellular organism from a single cell work? Why is it that when a human embryo develops at a certain stage, something similar to fish gills can be observed?

Yes, and just a curious man in the street, not burdened with the details of organic chemistry, such questions are not avoided.
')
That would have been a toy designer, with which you can collect simple growing organisms. Then, having built an extremely simplified model that demonstrates many of the phenomena of the living, one could get closer to the answers to the questions of the device of life, or at least to an understanding of where to look for these answers.



Such an extremely simplified and visual model can be “Live graphs” - finite automata on a graph, each node of which contains some executing device (automaton) with a finite number of states and with a set of primitive rules governing the creation or modification of new connections between nodes.



“Just see how I grew cabbage!” (C) Emperor and Downshifter Diocletian

The article will describe one of the embodiments of the “Live graph” - the cellular automaton for the deployment of the graph GUCA (Graph Unfolding Cellular Automata). You can “feel” the demonstration of GUSA right in the browser with the Silverlight plug-in connected. The web application visualizes the short life of some of my first copies of growing graphs — both personally designed products of “genetic engineering”, and “naturally selected” genetic forms.

Even if the initial graph consists of only one node, and all generating nodes of the graph will have the same copy of the rule set with each new iteration of the rules triggering, it will be possible to observe the development of a wide variety of structures. It is easy to see that the initial node is analogous to the embryo of a multicellular organism, the other nodes of the graph are similar to cells, the sets of rules are the chromosome, and the rules themselves are genes.

Origins

And it all started with a passion for artificial neural networks (ANNs), the study of which gave rise to the idea of ​​GUCA.

A small reminder. Artificial neural networks that have found widespread use in artificial control systems can be thought of as interconnected “neurons” that themselves perform fairly simple operations, for example, summing the incoming signals and transforming the resulting value. But being connected according to some rules into a single network, the “neurons” form a system, the capabilities of which significantly exceed the capabilities of its constituent elements - the same adder. The system as a whole already has functions of pattern recognition, classification, filtering of signals - all that is necessary for building a complex “intelligent” control system.

At the dawn of the use of neural networks, the network topology was set by the researcher, and the connection parameters were selected in advance by a predetermined algorithm using the accumulated data on the problem being solved. If for sufficiently simple types of neurons, the problem of building a network topology was sufficiently deterministic and solvable (which does not mean that the problem of the domain itself is solvable), then using cascades of neural nonlinear dynamic networks with feedback, this task turned out to be non-trivial and the idea arose to entrust the construction topology of the neural network computer. Came to the aid of methods, peeped in nature itself.

We are talking about neuroevolutionary methods, in which genetic algorithms are used to build the topologies of neural networks.

Neuro-evolutionary methods

The review of such methods was recently published on Habré: [1] habrahabr.ru/blogs/artificial_intelligence/84015 ,

I will not retell the already known methods for implementing such algorithms, I will only recall the main provisions of indirect coding of networks / graphs that also underlie the GUCA method under consideration, the implementation of which differs only in locality, contextual choice of the rules applied and “programmed death”.

In indirect methods of coding neural networks, in the “genome” of an instance of a network, the topology is not specified by an explicit listing of nodes and connections, but indirectly through the rules for constructing a network from its small fragment. After all, it is in this way that the organism of an animal develops from a small embryo, and indeed the human brain.

I also recall that the genetic algorithm provides: random generation or modification of codes, evaluation of the “result” of decoding the “genome” (that is, evaluation of the resulting neural network using a fitness function) and selection of the best representatives.

For neural systems that perform the role of object management systems (robots, manipulators), the fitness function may be the performance of the control object in a certain environment (labyrinth, handling objects, in flight, in battle, etc.)

At the same time, indirect encoding methods provide the following properties:

1) Modularity. Recursive construction of fractal structures according to simple rules and repetition of certain building blocks in the body structure.

2) Completeness. For any given network (graph), you can pick up the code.

3) Redundancy. The code may contain redundant data that does not affect the decoding result.

4) (Subject to use in context encoding rules)

a. Generation of topology depending on the signals passing in the neural network

b. Regeneration - recoverable with local damage

Review [1] shows that the main efforts of researchers are aimed at inventing more or less successful methods of coding network topology, rather than designing the principles of a neuron / network and coding its parameters, which is not surprising - it is the topology that determines the work of the entire system. neural network".

Topology Cultivation

Indeed, it would be useful to single out the problem of “growing” the network topology using the same genetic algorithm and indirect coding (in fact, a directed graph, and abstracting even more from the NA — an undirected graph). A fitness function (determining the success of an instance's survival) will no longer be the ability of a neural network to cope with managed objects, but, for example, the geometric properties of a topology. If the graph is expanded on a plane or in space, then the properties of the resulting image, including raster.

The concentration of efforts on a narrower task (building topologies, abstracting from the neural network) will allow :

• Find a wider application in areas other than ANN (auto-assembly mechanisms, the configuration of distributed computing in a computer network or viruses, the interaction of combat robots).

• Visualize the result (not only final, but also intermediate) for the researcher, which can help in the development of algorithms to better understand cause-effect relationships. In addition, a visual representation can suggest ideas / solutions / dead ends.

• It is more objective to compare different topology coding solutions or combine successful topology coding solutions with various “neuron” designs. Objectively - that is, regardless of the specific application domain.

• It is easier (faster and cheaper) to calculate fitness functions (as compared to assessing the suitability of a neural network as a control system) - i.e. it is to investigate topological algorithms, without spending additional resources, including computational ones, on derived tasks.

At the same time, such curious properties as the above-mentioned “modularity”, “regeneration” - will remain available for research.

It can be added that the evolution of the brain of animals also originates from the result achieved by the evolution of the form of a multicellular organism (axisymmetry - cartilage - spine - spinal cord - asymmetry - brain brain seal).

One of such methods is the cellular automatic deployment of the graph GUCA, the principles of which will be described in the next section.

Cellular automatic deployment of the graph GUCA (Graph Unfolding Cellular Automata)

The “living graph” of GUCA is a finite cellular automaton in which each node is in one of the states (the number of states of course) and can move to another state according to certain rules, depending both on the state of the node itself and on its environment. These rules are the same for all nodes, they are constant in time and are processed synchronously for all nodes simultaneously.

The classic representative of the cellular automaton is the “Life” game . The main difference between “Live graphs” and the classic game “Life” and its variations is that the “intracellular” automata are not located on a rectangular plane, but are located at the nodes of the graph with a variable number of connected neighbors.

At the same time, unlike most of the coding methods of the network topology described in the review [1], the “Living Graph” GUCA professes the following principles:

• Contextual selection of applicable rules

• Only local and one-step changes.

• Not only birth, but death

Strangely enough, all these features are inherently inherent in the “Life” cellular automaton, although they were chosen as a result of a long search for sets of rules and operations that solve the problem
graph deployment is the most simple and complete.

However, the removal operation was offered in one of the lecture exercises [2]

Principles

So, in the “Live graph” GUCA node is in one of the states . And there are rules according to which under certain conditions of operation operations are performed on the graph.

An example of a set of rules that satisfy the above-described “meta-rules” for some instance of a “live graph” is the following list:

1. "If the node is in state A, then create a linked node in state B"

2. "If the node is in state B, and the number of links is less than two, then create a linked node in state B"

3. "If the node is in state B and the previous state was B, then go to state C"

four.…

A state is one of the elements of a finite set. You can denote the number or letter of the alphabet - A, B, C, D, ....

Operations It is clear that it is possible to carry out a variety of operations on graphs - add / divide nodes, replace nodes with a related group, combine nodes. I stopped at four primitive operations, which seem to be quite enough to reproduce any arbitrarily complex structure.

• Transition of the node to the state X (thus, the state X is the operand of the operation)

• The birth of a new node associated with the current. The status of the new node X

• A node is connected to the nearest un-connected node in state X

• Disconnecting a node in state X

Now about the conditions that dictate the operation in the rule. I was not limited to the dependence on the current state of the node and the number of links between this node and other nodes. To these conditions added dependencies on the previous state of the node and dependence on the number of parents / divisions of the node (after all, each node, according to the list of operations, is generated by one and only one node-parent).

Conditions:

• The node is in state X

• Previous node state is Y

• Number of node connections - from C1 to C2

• The number of ancestors of the node (from which it was born) - from P1 to P2.

The last condition and the counter of the number of node divisions (an analogue of telomerase ) are introduced to ensure the development of the whole organism and / or its individual modules stop.

I also considered the operations “connecting a node with all nodes in state X”, “node death” - but I considered them redundant. I am also thinking of introducing the operation “resetting the counter of divisions”. I note that all operations are local and “rotate” around a node (they change only the node or its immediate environment).

However, perhaps the reader will be able to find a more coherent system of rules.

Grammar rules

GUCA rules can also be written in a short form, denoting the current state as a letter, the previous one with a letter in brackets, the number of neighbors with the “c” symbol (from connections), the number of parents - “p” (from parents). If the previous state is ignored in the condition, then we will indicate a dash in brackets. Let us divide the rule of operation from conditions by a colon symbol, and we denote possible operations as follows:

• The operation of transition to another state X is denoted by X

• The operation of the birth of a connected node is denoted by ++ X

• The operation of connecting to the node X is denoted by + X

• The detachment operation from node X is denoted by –X

Then, for some instance of a “live graph,” a set of rules will be written using the grammar:

1. A (A), p = 0: ++ B
2. B (-), c <2: ++ B
3. B (B): C
4. A (A): G
5. C (B), c = 1: G
6. G (G), c <5: H

If the initial node of the graph is in the state “A”, then after 12 consecutive iterations of the application of the rules, we get the “Finger dumbbell”:



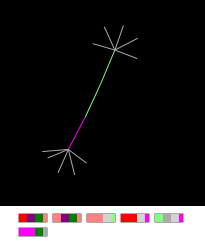
Figure Graph "Finger dumbbell" and the conditional display of its gene map.

This is the very first graph that I designed several years ago to debug a finite state machine on graphs. It is so simple and clear that I mention it only in order to pay tribute to the pioneer. The rules laid down in its “genome” are simple: from the node with the initial state A, a short thread is born that ends with nodes (in the G state) for which the rule is triggered: while the number of neighbors is less than or equal to five, create a new neighbor.

Hereinafter, when displaying a graph on a plane and on a conditional display of a gene map, red indicates the state A, pink - B, green - C, crimson - G.

Turning off the gene number 5 of the "finger dumbbells" you can create a "freak" - "ordinary hand":



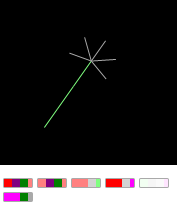
If you turn the gene back, the second "hand" will grow back.

Thus, a set of simple rules can define the topology of a graph. Generally speaking, the topology of a graph determines not only the set of rules and the initial state of its node (s), but also some global constraints — for example, the maximum number of iterations or the maximum possible number of connections of nodes.

Idea check

One way to make sure that the system of rules described above is sufficient for constructing graphs of any topology is to solve “control problems” for construction. Having thought of this or that figure, try to come up with a “gene”, from which it will be born. And if the conceived figure cannot be constructed in any way, then the rule system is unlikely to be suitable not only for growing graphs, but also for constructing a complex artificial neural network.

On the one hand, “control tasks” should be extremely simple, on the other hand, “indicative” (please do not confuse with “spectacular”) to demonstrate the qualitative properties and effects of a complex living organism - modularity, hybridization, self-healing ... whimsical, finally. Such examples can be - the simplest fractals, the figures growing from within, the grids with a large number of cells and simply “wild” plants.

Some of these tasks were extremely difficult (long) and unreliable (the answer often did not converge) to solve in mind or on paper, and in order to carry out these first experiments, I had to arm myself with an “experimental setup”.

Experimental installation (Silverlight application)

This experimental setup was a software application that allows you to debug the "genetic code" and the playback machine. In addition, with its help you can:

• visualize the process of graph growth,

• visually display the color "map" of the chromosome and the activity of genes in the process of graph growth

• look at what the shutdown of one or another gene or cutting the “live graph” will lead to.

The demonstration Silverlight version of the “experimental setup” is available at http://roma.goodok.ru/guca/GUCA_DemoSL.html



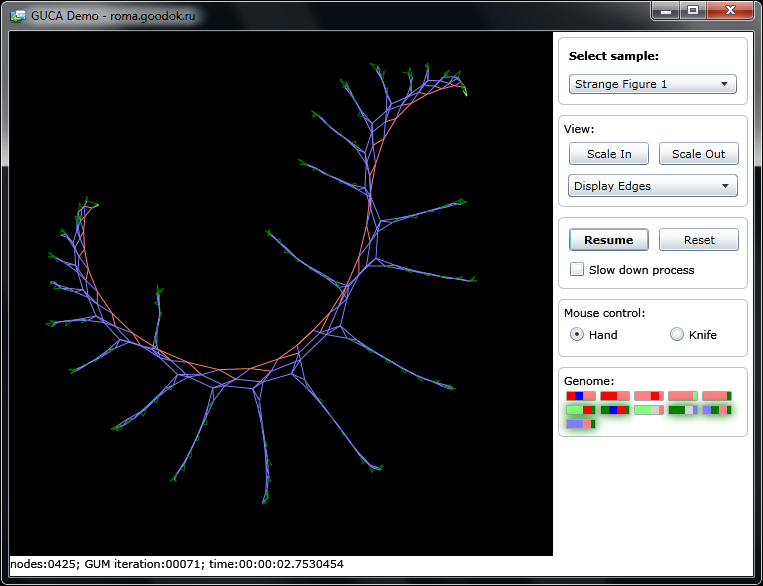
The Silverlight version of the Experimental Setup for growing a graph makes it possible to observe the development of a graph, the activity of genes on a chromosome map, and to cut individual branches with a knife.

To start the graph expansion, you need to select an example (Select sample) from the drop-down list on the right “control panel” and click on the start button (“Start”).

In the central area with a black background, the graph will be displayed during its growth from a single germ node. Different states of nodes are displayed in the corresponding color You can change the scale and appearance of the display or slow down the growth of the graph to view the details of the process.

You can not only observe the development and life of the graph, but also intervene in this process by incising with a scalpel (Knife switch) or turning off one or another gene, bringing to light “freaks”, achieving “fatal outcome” or “cancerous swelling”

At the bottom right , a chromosome “map” (“Genome”) is conventionally displayed - each rectangle on it corresponds to a “gene” (paragraph of the rule). Again, the states of the nodes in the rule condition, the rule itself, and the node state in the rule operand are color coded. In the process of growth of the graph, green genes mark those genes that were active during the next iteration of the rules execution.

Hovering the mouse on the rectangle of a separate "gene", you can see the decoding of the rule encoded by the gene in the form of text, and by pressing the mouse button, turn off (or turn back) the selected gene.

In this article I will not dwell on the description of the “laboratory setup” device, although by itself its “assembly” was a very interesting occupation - besides graph theory and discrete mathematics, knowledge and experience in the numerical solution of equations of mathematical physics, geometry, etc. were useful. besides, its genetic “source” code itself is a result of evolution and contains the heritage of distant ancestors - after all, the first version and design solutions were implemented on Delphi 7.0. You could even say this is my first “Hellow World!” On the Silverlight | WPF platform. I will only note the use of the QuickGraph libraries (graphs and algorithms) and AForge (the genetic algorithm).

The simplest examples

So, let's look at some of the simplest examples of “live graphs” that demonstrate living properties. Some of the specimens (for example, the aforementioned "finger dumbbell") were designed only as a divine beginning for the world of living graphs (i.e., Me), others are the result of evolution, and still others are genetically modified products.

"Hairy Circle"

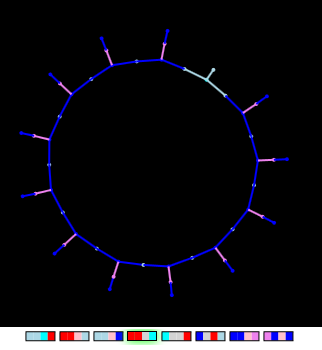
This figure is a genetically modified product! First, using the genetic algorithm, an infinitely growing inside circle was obtained (the fitness function depended only on the topological characteristics of the graph — the obligatory presence of two faces). Then another “gene” was added - the “hair gene” (rightmost on the gene map)

By launching an “organism” growing from within, one can observe how individual segments of a circle appear as a result of cyclic repetition of insertion operations of new edges.

"Finger circle" (hybrid)

If we take the “dumbbell” and “hairy circle” genes and combine them in one chromosome of the “embryo”, then a hybrid will arise from it, inheriting both the properties of the “dumbbell” and the “round” properties:



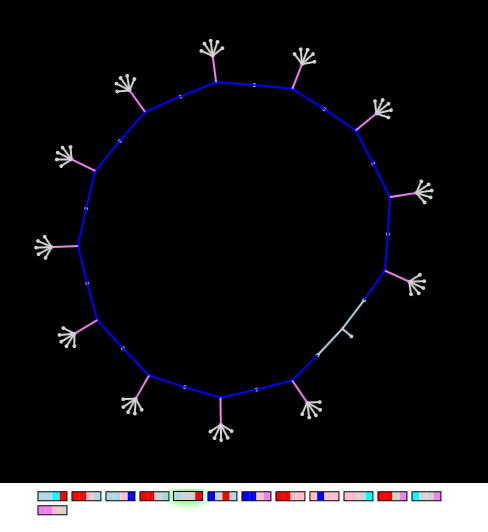
Figure: Hybrid "finger dumbbells" and "hairy circumference" has common properties

Please note that some of the “dumbbell” dummy genes remain inactive during the entire process of graph deployment (on the gene map, gene activity is indicated by a green light).

"Bushes" (Fractals)

The simplest genetic code of two "genes" creates an arbitrarily large graph. " If you cut off any of its branches, the "bush" almost instantly recover in the same size and shape.



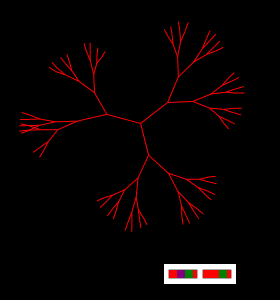
Figure Primitive fractal is given only a pair of genes

"Kokoshnik (rectangular mesh)"

This and the next two strange figures are the result of my attempts to construct a square grid in the form of a square.



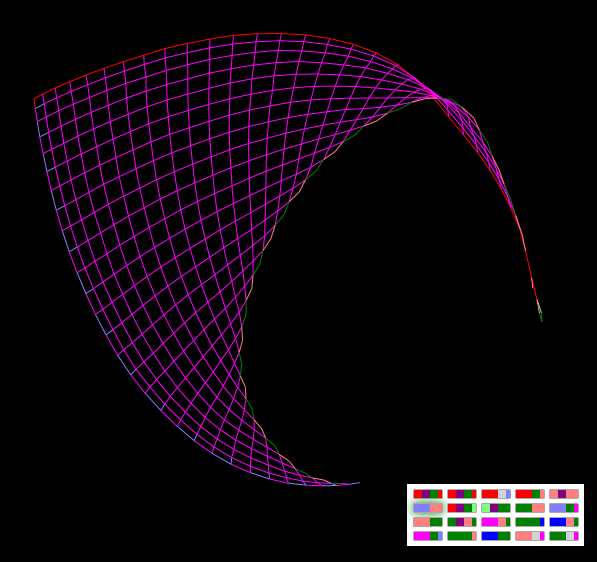
Figure "Kokoshnik" - expanding a rectangular grid

By changing a pair of genes, one can grow an arbitrarily large (and small) mesh. A knife can make holes. Try to turn off the gene №13 "O (O): + L" and turn it on after deployment.

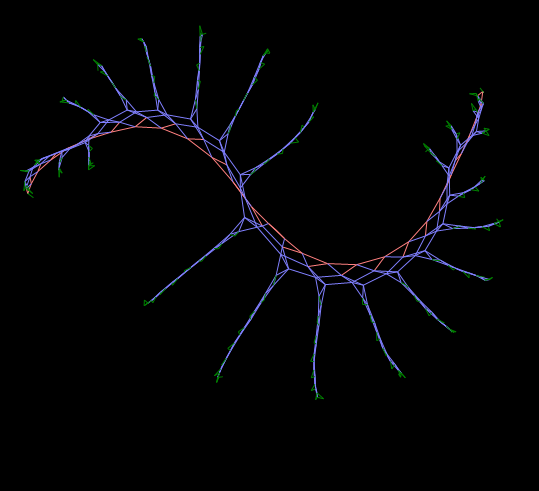
"Strange Figure 1" and "Strange Figure 2"

“Strange Figure 1” is my mistake. In fact, the goal was to create an equilateral square grid. The figure is depicted at the very first figure in the article (Figure 1). If, however, cutting its processes directly on a live graph, then, having released new processes instead of cutting, the figure will take a more extended form:



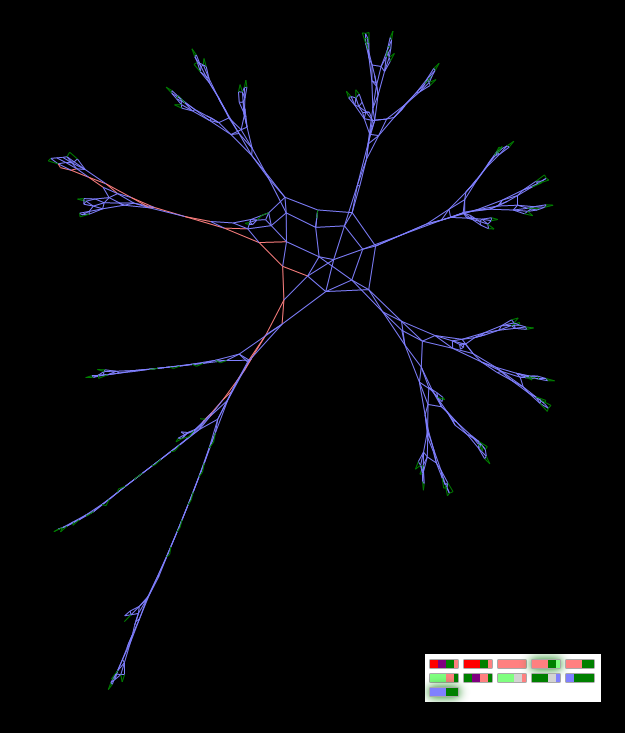
Figure "Strange figure" after circumcision

Strange figure 2 . The chromosome of this figure differs from the chromosome of “Strange figure 2” by just one gene, more precisely, even a part of the gene (close relatives), but the form of the “decoding” result is a little like the form of the previous instance.



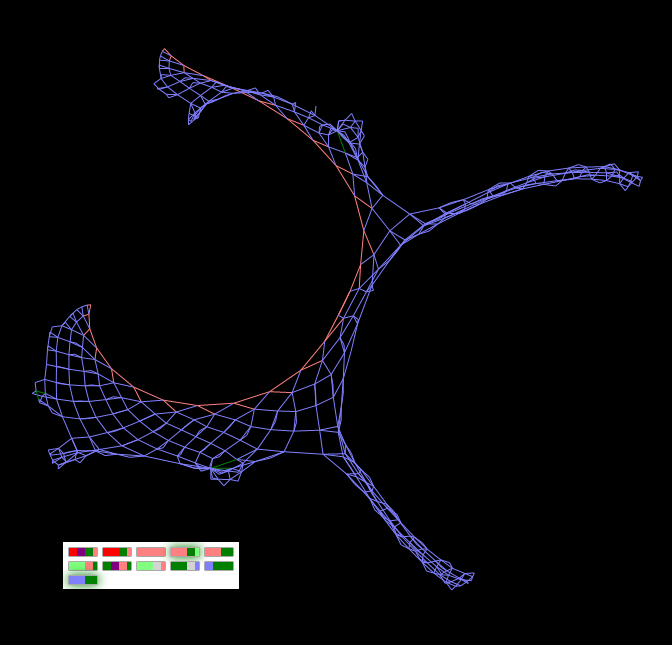
"Strange figure 2" - a close relative of "Strange figure 1" - differs in only one gene

"Hexagon with spikes" (the result of evolution)

It took thousands of iterations of the genetic algorithm to get 10 genes of this figure. The fitness function in Russian sounded something like this: “the closer the number of faces to two, and the number of nodes of degree 1 to six and the number of nodes of degree 3 to six and the number of genes to zero - the more chances a graph will survive” (the degree of a node is the number connections)

The evolution of this species has experienced several jumps: a triangle, a square with processes, a six square with irregular processes, and, finally, a regular one. Slowing the process of unfolding, you can see what solution evolution has found to build a shape.



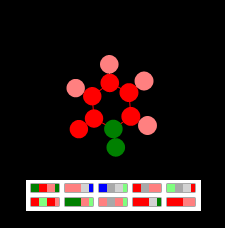
Hexagon drawing with "leaves" - The result of the genetic algorithm

Conclusion

So, we have seen how using such abstract objects as finite automata and graphs, we can create systems that are amusingly similar to multicellular living organisms, which demonstrates the common principles underlying the "living graphs" and in the laws of formation of geometric forms of the living.

However, this does not mean that we have revealed the secrets of life. It simply means that you can move on: explore the patterns of the evolution of "live graphs". Let me remind you that in the demonstration application we observed “ontogenesis” and the result of evolution, and not evolution itself.

Issues of further research can be both the determination of the boundaries of the “live graphs” model, and the search for quantitative and qualitative patterns in an unencumbered evolutionary model with excessive details (dependence of gene lengths on the complexity of forms, statistics of genetic information on the position of a species in the evolution tree, the rate of evolution on the set of valid operations, etc.).

According to the results of these studies, determining the most effective evolutionary algorithms, you can try to apply "live graphs" in the source area: in artificial neural networks or in the study of the evolution of robots, "animats", artificial control systems.Of particular interest is the combination of dynamic nonlinear neural networks with live graphs, in which the state of excitement of the neuron is one of the states of the finite automaton "inside" the live graph. It will be possible to observe something like a “genetic memory.”

Also, it would be curious to create a material embodiment of living graphs in the form of a self-organizing colony of primitive robots, the firmware of which sews the genetic code of the community.

All these areas are difficult to reach for a solitary researcher, and I hope some of the readers will still make their own small and big discoveries in this field of research. Quite possibly, models like Live Counts will be the starting point for your own research. True, this will require other "experimental installations".

Literature

[1] “Review of Neural Network Evolution Methods” http://habrahabr.ru/blogs/artificial_intelligence/84015/

[2] “Evolutionary Computation for Modeling and Optimization” Daniel Ashlock, January 12, 2004 http: //orion.math. iastate.edu/danwell/ma378/

UPDATE Added the ability to load the “genome” from xml. Example file: the “strange figure 1” genome . Now you can try to grow your graphs, check your ideas ... finally find mistakes.
UPDATE 2 Laid out the source (1.8Mb) with release build.