When trigonometry is not needed
Looking through the different code for displaying some even primitive graphics, I noticed that some programmers had an excessive love for trigonometry. Often the code is replete with sines, cosines and arctangents where you can do without them. Even good programmers who are able to design a complex system, but for some reason have not mastered the vector in the scope of the school program, are sinning with this. Literally, the basics of vector algebra is enough to solve many pressing problems. In this topic, I want to conduct a brief educational program, recall basic actions with vectors on a plane and, as an example, solve two problems without trigonometry: search for a reflected beam along the incident beam and an arbitrarily arranged mirror, as well as drawing the arrowhead. If you can imagine drawing a randomly directed arrow without sines and cosines in your head, feel free to skip this topic. For the rest I will try to explain easier.
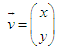
Geometrical meaning is a segment on a plane for which length and direction are important, but position is not important. That is, parallel transfer does not change the vector. It is often useful to identify a vector with a point (x, y) on a plane — it’s like drawing a vector from point (0,0) to point (x, y). Consider the basic operations.
Addition of vectors:
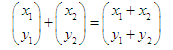
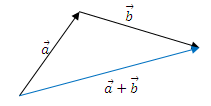
The geometrical meaning is depicted in the picture - we move the second vector so that its beginning coincides with the end of the first, and the result is the vector from the beginning of the first to the end of the second:
Vector multiplication by scalar (number):
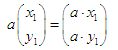
Geometrical meaning is the elongation of a vector by an appropriate number of times, without changing direction (except for the opposite, if a is negative). Multiplication by -1 will reverse the vector by 180 °, without changing the length. Dividing a vector by a is multiplying by 1 / a .
Dot product of vectors:

Very important thing. Multiplying two vectors, we get a number that characterizes the length of the projection of one to another. By multiplying two vectors, by the sign we can determine whether the vectors are directed in one direction (the scalar product is positive), are directed oppositely (the scalar product is negative), or are perpendicular to each other (the product is zero). You do not need to calculate the arctangents of the relationship of the coordinates of each vector and compare the angles. Two multiplications, one addition and a hat.
It is also important that the scalar product of the vector itself on itself is the square of its length (a consequence of the Pythagorean theorem):
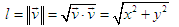
A vector is called normalized or unitary if its length is equal to one. To normalize an arbitrary nonzero vector is to divide it by its length. It turns out a single vector, consistent with the original.
The scalar product of an arbitrary vector by unit will give the exact length of the projection of this vector on the direction of unit. To get not just length, but the projection vector itself, you need to multiply this length by our unit vector:
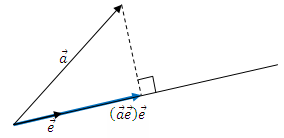
In parentheses the scalar product of vectors a and e , and then multiplication of the vector e by a scalar.
What if we need a projection on a non-normalized vector? To ration, it is necessary to extract the root, and this is long and sad. However, if we take a closer look at the formula, we will understand that we need to divide the result by the square of the length, that is, simply by the scalar product of the vector by itself. That is, the projection of a onto an arbitrary nonzero b will be calculated as follows:
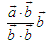
The scalar product of two unit vectors is the cosine of the angle between them. If suddenly you still needed an angle between the directions, check, maybe you don’t need the angle at all, but its cosine (or sine, which in some cases can be obtained from the main trigonometric identity). Then you do not need to poke around with arctangents.
That is, in fact, the whole basic theory. Now we will try to apply it.
Knowing that the angle of incidence is equal to the angle of reflection, you can come up with some kind of naive algorithm:
However, if you think by vectors, then a simple geometric construction gives a significantly faster solution:
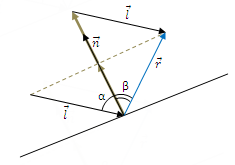
Two projections of the vector l onto the normal with a minus sign and plus one more vector l will give us exactly the result:
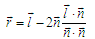
It is not necessary to divide, if the normal is already normalized. By the way, I did not tell you how to define it. If the line is given by two points (x1, y1) and (x2, y2), then the normal vector (unnormalized) is easily defined like this:
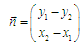
Sometimes the normal sign is important to know which side of the straight "external". In our problem, it does not matter, you can easily verify this.
By the way, the resulting formula of the reflected beam acts in the three-dimensional version, only the normal should be determined already for the plane.
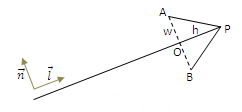
Here the point (x2, y2) is designated by the letter P. It is necessary to calculate the coordinates of points A and B in order to draw the segments PA and PB. We assume that we are given the longitudinal and transverse lengths of the antennae h and w . The attentive reader can already propose an algorithm: to find the point O, you must subtract from P h multiplied by the unit vector along the arrow (here, it seems, you cannot do without a root, but you need it only once!). And then A and B are already determined, adding to O the normal vector multiplied by w and - w . Notice that we never defined the angle of the arrow solution anywhere (in general, it is the arctangent of the ratio w and h ), but we don’t need it: the arrow is easily drawn and so.
')
Theory
So, a vector (we consider only the two-dimensional case) is a pair of numbers: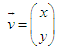
Geometrical meaning is a segment on a plane for which length and direction are important, but position is not important. That is, parallel transfer does not change the vector. It is often useful to identify a vector with a point (x, y) on a plane — it’s like drawing a vector from point (0,0) to point (x, y). Consider the basic operations.
Addition of vectors:
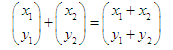
The geometrical meaning is depicted in the picture - we move the second vector so that its beginning coincides with the end of the first, and the result is the vector from the beginning of the first to the end of the second:

Vector multiplication by scalar (number):
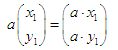
Geometrical meaning is the elongation of a vector by an appropriate number of times, without changing direction (except for the opposite, if a is negative). Multiplication by -1 will reverse the vector by 180 °, without changing the length. Dividing a vector by a is multiplying by 1 / a .
Dot product of vectors:

Very important thing. Multiplying two vectors, we get a number that characterizes the length of the projection of one to another. By multiplying two vectors, by the sign we can determine whether the vectors are directed in one direction (the scalar product is positive), are directed oppositely (the scalar product is negative), or are perpendicular to each other (the product is zero). You do not need to calculate the arctangents of the relationship of the coordinates of each vector and compare the angles. Two multiplications, one addition and a hat.
It is also important that the scalar product of the vector itself on itself is the square of its length (a consequence of the Pythagorean theorem):
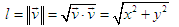
A vector is called normalized or unitary if its length is equal to one. To normalize an arbitrary nonzero vector is to divide it by its length. It turns out a single vector, consistent with the original.
The scalar product of an arbitrary vector by unit will give the exact length of the projection of this vector on the direction of unit. To get not just length, but the projection vector itself, you need to multiply this length by our unit vector:

In parentheses the scalar product of vectors a and e , and then multiplication of the vector e by a scalar.
What if we need a projection on a non-normalized vector? To ration, it is necessary to extract the root, and this is long and sad. However, if we take a closer look at the formula, we will understand that we need to divide the result by the square of the length, that is, simply by the scalar product of the vector by itself. That is, the projection of a onto an arbitrary nonzero b will be calculated as follows:
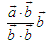
The scalar product of two unit vectors is the cosine of the angle between them. If suddenly you still needed an angle between the directions, check, maybe you don’t need the angle at all, but its cosine (or sine, which in some cases can be obtained from the main trigonometric identity). Then you do not need to poke around with arctangents.
That is, in fact, the whole basic theory. Now we will try to apply it.
Calculation of the reflected beam
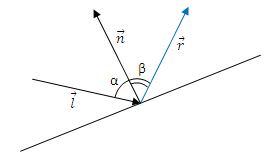
The reflected beam can be useful not only for optical problems, but also, say, when modeling an elastic collision of an object with a wall, which is indispensable for programming animated beauties. Then the velocity vector of the object will change just by the law of reflection. So, we have a falling vector l and some arbitrary straight line from which the reflection is produced. A straight line can be given, for example, by two points. It is required to determine the reflected vector r of the same length as l :
Knowing that the angle of incidence is equal to the angle of reflection, you can come up with some kind of naive algorithm:
- Calculate the difference between the coordinates of the points of the line, take the arctangent of their relationship - we get the slope of the line to the x axis.
- Similarly, determine the inclination of the incident beam to the x axis.
- Calculate the difference of these angles, subtract it from 90 ° - we get the angle of incidence.
- Add the angle of incidence twice and another 180 ° to the angle of inclination of the incident ray — we obtain the angle of inclination of the reflected ray.
- Calculate the length of the incident beam and multiply by the sine and cosine of the angle of inclination of the reflected beam - we obtain the resulting vector.
However, if you think by vectors, then a simple geometric construction gives a significantly faster solution:

Two projections of the vector l onto the normal with a minus sign and plus one more vector l will give us exactly the result:
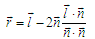
It is not necessary to divide, if the normal is already normalized. By the way, I did not tell you how to define it. If the line is given by two points (x1, y1) and (x2, y2), then the normal vector (unnormalized) is easily defined like this:
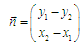
Sometimes the normal sign is important to know which side of the straight "external". In our problem, it does not matter, you can easily verify this.
By the way, the resulting formula of the reflected beam acts in the three-dimensional version, only the normal should be determined already for the plane.
Drawing arrows
Let the ends of the arrows (x1, y1) and (x2, y2) be given. Need to draw a mustache of a fixed size at the end (x2, y2). Let's see the picture:
Here the point (x2, y2) is designated by the letter P. It is necessary to calculate the coordinates of points A and B in order to draw the segments PA and PB. We assume that we are given the longitudinal and transverse lengths of the antennae h and w . The attentive reader can already propose an algorithm: to find the point O, you must subtract from P h multiplied by the unit vector along the arrow (here, it seems, you cannot do without a root, but you need it only once!). And then A and B are already determined, adding to O the normal vector multiplied by w and - w . Notice that we never defined the angle of the arrow solution anywhere (in general, it is the arctangent of the ratio w and h ), but we don’t need it: the arrow is easily drawn and so.
')
Conclusion
In general, trigonometry comes in less often. Without trigonometric functions, the refracted ray is calculated according to Snell's law. If you need to rotate a complex drawing at a certain angle, you only need the sine and cosine of that same angle. The rotation matrix is made up of them, and all points are multiplied by it in turn. Trigonometry is actually slow, especially when there is a lot of it. Therefore, do not use it where it is not needed.Source: https://habr.com/ru/post/105882/
All Articles