Dynamic programming method for counting the number of cycles on a rectangular lattice
This article is addressed to those readers who are engaged in programming algorithms, and is particularly interested in intractable problems. Those habrulyam who oppose the placement of algorithms on Habré should immediately stop reading this work.
In the article I will show how to use the dynamic profile programming method for solving the problem of counting the number of Hamiltonian cycles on a rectangular grid of size m by n. On Habré there are several articles on the topic of dynamic programming (for example, this one ), but nowhere is this a more complex application of the method. This approach can also be called the transfer matrix method, as you like.
I warn you that the article contains about 2000 words (8 A4 pages), but the road will be by walking.
')
What is intractable problem? This is a task that does not have an effective solution algorithm. Moreover, this is not necessarily a problem with an exponential complexity of the solution, the complexity can be polynomial, but with a sufficiently large degree of polynomial (for example, the problem of k queens, which I already wrote about here ). You can learn more about such tasks and their classification in the classic book by M. Gary, D. Johnson “Computing Machines and Intractable Problems”.
Such problems are usually solved by brute force, dynamic programming and combinatorial analysis methods. Often, an acceptable solution is obtained by using these three components at the same time, but this also requires the experience of writing a sufficiently optimal code. It’s very good if you have a cluster of at least several thousand cores and at least a couple of hundred gigabytes of RAM. Unfortunately, I'm not kidding, many tasks can be solved only on such a machine ...
I like to solve intractable problems and I even organize contests for programmers-mathematicians on this topic from time to time. This article is partially confined to the “ Pre-Hamilton cycles ” competition, which began on October 1 and ends on October 31, 2010. The problem proposed in the conditions of the competition is solved by me using the same method (with minor changes), which will be described here.
In the section with the conclusion of the complexity of the algorithm, it is assumed that the reader knows the elements of combinatorics (what is the number of combinations, for example), and in the section about the finite state machine the reader will be forced to recall elements of graph theory (for example, what is the adjacency matrix of the graph, and what does power).
In the work there is a graph, called a rectangular lattice P m × P n . A rectangular lattice is an integer point of the coordinate plane, connected by the principle of the nearest neighborhood. The designation P m × P n is related to the fact that the integer rectangle is the direct product of two chains, the first of which has m links (denoted by P m ), and the second one - n (denoted by P n ). The number m is the width of the lattice (length from left to right), and n is its length (length from bottom to top).
A Hamiltonian cycle in a graph is a cycle that passes through each of its vertices exactly once. In fig. Figure 1 shows an example of a Hamiltonian cycle on a P 6 × P 8 lattice.

Figure 1 - Example of a Hamiltonian cycle on a 6 × 8 grid
The task is to find the number of Hamiltonian cycles on the lattice P m × P n for given m, n ≥ 2. For example, the following figure shows all 6 Hamiltonian cycles on a 4 × 4 grid.

Figure 2 - All 6 Hamiltonian cycles on a 4 × 4 grid
Any cycle in the P m × P n graph can be built sequentially along the “layers” of P m × P k (k = 0,1,2, ..., n). For clarity, in Fig. 3 shows a line cutting the graph into two parts. Below it, the graph P 6 × P 5 , on which the still unfinished “cycle” is a set of disjoint simple chains. This constructed part of the cycle will be called the "past." At the top of the line, one of the possible options for the completion of an unfinished “cycle” (this is the “future”) is depicted. The cycle is closed and does not touch the cut line at its points of inflection. And since, bypassing the cycle in any direction, we will return to the starting point, the cut line will be intersected by the cycle an even number of times.

Figure 3 - Cycle section
The intersection of the cycle by the cut line itself can be represented as a regular bracket sequence, discharged with zeros. For example, in fig. 3 such a sequence has the form (0000) . In this sequence, a pair of matching opening and closing brackets correspond to the two ends of the same chain through the “past”, and the zeros mean that at these points there is no intersection of the cut line with the cycle. Thus, any section can be encrypted with the correct bracket sequence discharged with zeros. Since the initial and final cuts must be zero (consisting entirely of zeros), we must distinguish them, denoting one with a line below, and the second with a line above.
In the process of building a cycle, we do not need to know either the "past" or the "future", but it is enough to store only information about which section at a given time has turned out, and how the rest can be obtained from this section. Indeed, how to move from the current cut to the next? For example, as in fig. 3 is the transition from the cut (0000) to the next cut 00 () 00 ? This will be shown in the examples.
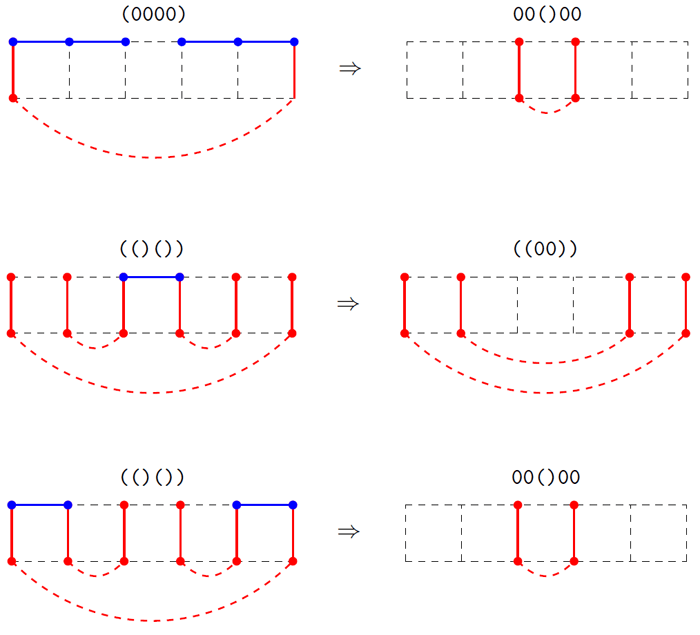
Figure 4 - Examples of the transition from one section to another
In fig. 4 shows 3 examples of transitions from one section to another. The arcuate lines show that the ends of the corresponding vertical arcs are connected through the “past”. The first case shows the transition to fig. 3 The remaining two cases are slightly more complex, but they clearly demonstrate what new cuts can be obtained by adding different combinations of horizontal arcs.
However, not all combinations of horizontal arcs can lead to a new cut. Some combinations may be unacceptable for three reasons, indicated in Figure 5.

Figure 5 - Examples of invalid transitions. Three possible cases
In the first case, one of the three chains closes ahead of time, so the Hamiltonian cycle cannot turn out. In the second case, three arcs meet at the same vertex. Finally, the third case is impossible due to the fact that some vertices were unused (and the Hamiltonian cycle must go through all the vertices).
So, suppose that we have information about all possible sections of our lattice and which sections from which can be obtained by including horizontal arcs. All this information can be represented in the form of a finite automaton whose nodes will be cuts, and the arcs will show the possibility of a transition. In fig. 6 shows an example of such a finite automaton constructed for a 3 × n lattice.
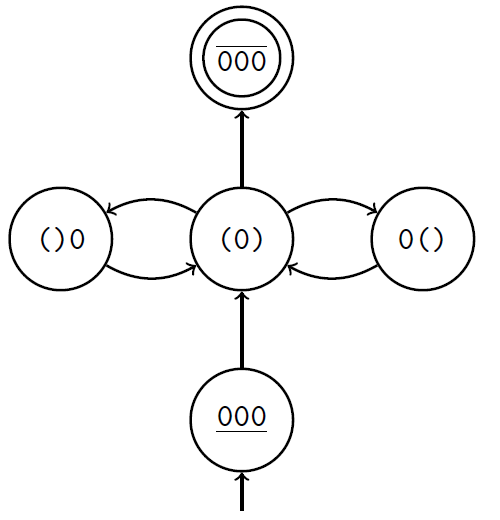
Figure 6 - State machine for the 3 × n grid
The answer to the question of how many cycles exist on the P 3 × P n grid will be the number of ways to go from the initial state of the automaton to the final state in n steps. How to do it? I know two ways: bad and better. I'll start with the bad.
One of the ways to solve the problem is called the transfer matrix method, which consists in the following. Let us enumerate all possible cuts from 1 to N in any way, but so that the initial state is number 1 and the final state is number N. We construct a matrix T in which the numbers T ij will be equal to the number of ways to get from the cut i number cut j . The solution of the problem for the lattice P m × P n is the number (T n ) 1, N.
For example, for the P 3 × P n lattice, we have already constructed an automaton (Fig. 6), so we can write out the transfer matrix.

Figure 7 - Transfer matrix, or adjacency matrix of the finite automaton of fig. 6 and her sixth degree
In fig. 7 shows the transfer matrix T for Hamiltonian cycles on the P 3 × P n lattice. The solution will be the number (T n ) 15 . For example, (T 6 ) 15 = 4, so is the number of Hamiltonian cycles on the P 3 × P 6 lattice.
However, in practice this method of solving the problem is applicable, at most, for m = 12, when the transfer matrix for Hamiltonian cycles on the lattice has a size of 3774 × 3774 (see Table 1 in the discussion section) and fits in the RAM of a personal computer. Long numbers are stored in the matrix itself, since, for example, the answer for the P 12 × P 20 grid contains 33 digits, and for the P 12 × P 100 grid, the number of digits reaches 174.
In the section “Modular arithmetic” it will be shown how to get rid of long numbers, sacrificing the speed of calculations, but it still will not save from the monstrous growth of the transfer matrix. Therefore, I called this method of solving the problem bad.
This solution, as it is not strange, is also called the transfer matrix method, but the matrix clearly does not appear in it, therefore, this method is called in the Russian-language literature a method of dynamic programming [on a finite state machine].
The meaning of the method is to store the number of ways to get to each vertex of the finite state machine in k steps. At step k = 0, this number is 0 in all vertices except the starting one. The number of ways to be at the starting vertex at step k = 0 is, by definition, set to 1. Let at some step k at vertex i you can be P ways, then going to step k + 1 we add the number P to the number of ways it is at all vertices j, which can be reached from i. But for this you need to know which vertices you can get from i, that is, to store the matrix again! In fact, it is not necessary: getting to vertex i, and knowing what section it denotes, we re- build all such cuts that can come out of it.
How this is implemented in the program is an individual matter. I will explain my approach. Suppose there is a queue Q in which cuts are stored (as a bracket sequence) and the number of ways to be in them. At the beginning of the algorithm, a section consisting of zeros and a number of methods equal to 1 is stored in the queue. Along with the queue, there is a hash table that also stores sections and the number of ways to be in them. At the beginning of the algorithm, the table is empty.
At step k, we get another section i from the queue, and the number of ways P can be in it. We build the set J of all possible cuts obtained from i. For each j of j, we check if it is in the hash table. If not, add j to the table along with the number of methods P. If yes, then from the table we take the number of ways Q that can come in j and write the number P + Q in its place. The exception is the case when j is equal to the zero cut, which means that we got to the final state and have to add the number P to the answer, but not add the zero cut to the hash.
At the end of step k, the queue is empty, so move the data from the hash table to the queue, clear the hash, and go to step k + 1.
I am using a hash with open addressing and double hashing. The number of collisions is 0.6 per call. That is, in 60% of cases, one step is taken on the table, and in other cases it falls right away. I think this is a good hash for such a task.
First, I will point out the upper limit of complexity, and then I will show what actually happens in practice.
The set of all regular bracket sequences discharged with zeros and having length m are Motzkin words of length m over the alphabet { 0 , ( , ) }, generated by context-free grammar
Z → Y | Y ( Z ) Z,
Y → ε | 0 Y,
where ε denotes an empty word. The number of such words can be calculated from combinatorial considerations:

In this formula, k is the number of pairs of brackets. The first expression under the sum sign (the fraction and the very first binomial coefficient) is the Catalan number , which shows the number of regular bracket sequences, and the second binomial coefficient is the number of ways to put 2k brackets in m positions (filling the remaining positions with zeros).
Thus, the number of all possible cuts for Hamiltonian cycles on the lattice, at least, does not exceed the number of Motzkin words, and Motzkin words grow at a speed of almost 3 m . In fact, such cuts are much smaller, since some may be unacceptable. For example, cuts such as (0) 000 or (() 0) 0 will be unacceptable for a lattice of width 6, since they cannot be obtained when constructing a Hamiltonian cycle. The discussion section will show the table. 1, which indicates the total number of cuts for some m. In reality, it turns out that only a third of Motzkin's words are permissible, and taking into account symmetry, it is enough to store only one fifth of them.
I will explain. Some cuts are palindromes and coincide with themselves with symmetric reflection, but those that are symmetrical to each other can be stored as one section. For example, the cut (()) () and () (()) can be considered one and the same. With this in mind, it turns out that, on average, only one-fifth of Motzkin's words should be stored in the program.
For each section, we have to go through 2 m-1 ways to put horizontal arcs. And all this together we have to do n times.
Total, the algorithm has complexity O (6 m · m -1/2 · n). And in fact, due to the fact that many cuts are unacceptable, in practice the complexity of the algorithm is O (5 m · n). This happened during my observation of the algorithm.
As for the memory used, the main part of the resources is occupied by the queue and the hash table. Each section for m≤32 can be stored in a 64-bit integer, since 2 bits are required for storing brackets and the number 0. Plus a long arithmetic that eats up all the resources completely. But there is one technique that allows you to slow down the calculations, giving up long arithmetic.
Let's calculate the answer modulo various primes: 2 31 -1 = 2147483647, 2147483629, 2147483587, ... To do this, the program must be run as many times as we can choose different modules (although, of course, you can count on 2-3 modules at once, in memory). According to the Chinese remainder theorem, it is possible to recover the answer up to the product of all primes used. If the product of all primes is greater than the answer to the problem, then the answer is uniquely restored. How to choose the required number of modules?
For example, let's count the number of cycles on a 16-n grid on two modules. Let n = 1,2, ..., 16. Then get the answers
[0, 1, 128, 405688, 24980352, 776813457, 729683652, 1087605227, 2000673777, 456710131, 1550214608, 568568229, 2047094091, 1175631455, 380271385, 1536681549] (mod 2147483647).
[0, 1, 128, 405688, 24980352, 776813727, 729709644, 1107434405, 301217473, 1373982040, 103268356, 218837622, 1185113726, 2085126539, 1315887233, 2008046410] (mod 2147483629).
According to the Chinese theorem on residues, we have:
[0, 1, 128, 405,688, 24,980,352, 32,989,068,162, 3101696069920, 2365714170297014, 309656520296472068, 2415277789552788286, 3926649012293853406, 726889843182193849, 153366515247378747, 1645735649663585962, 3698490188721496226, 1337259901989820598] (mod · 2147483647 2147483629).
How to check if we have enough 2 modules? In this problem, it is clear that numbers must grow exponentially, which means their logarithms must grow linearly. Take logarithms (for example, natural):
[-INF, 0, 4.852, 12.91, 17.03, 24.22, 28.76, 35.40, 40.27, 42.33, 42.81, 41.13, 39.57, 41.94, 42.75, 41.74].
The logarithm of the product of our two modules is 42.98. We see that the difference between the numbers monotonously grows by about the same amount, and, starting with n = 9, for some reason they stop growing. Moreover, in this place the limit was reached, beyond which the numbers can no longer be. This means that two modules were not enough. Let's take 4 modules and restore the answer:
[0, 1, 128, 405,688, 24,980,352, 32,989,068,162, 3101696069920, 2365714170297014, 309656520296472068, 168435972906750526954, 27738606105535271640888, 12142048779807437697982030, 2344813362310160031818110686, 888511465584607682074513271223, 191678405883294971709423926242394, 65882516522625836326159786165530572] (mod 2147483647 2147483629 · · · 2147483587 2147483579).
Logarithms are:
[-IFN., 0, 4.852, 12.91, 17.03, 24.22, 28.76, 35.40, 40.27, 46.57, 51.68, 57.76, 63.02, 68.96, 74.33, 80.17].
The numbers strictly increase, increasing by about the same amount. The logarithm of the product of 4 selected modules is 85.95, which is noticeably more than the last number in the sequence. That means the answer is correct. You can verify this by typing the query "65882516522625836326159786165530572" in Google.
With this algorithm, I was able to calculate the number of cycles on a 22 × 100 grid. Calculations on a single module lasted about 30 hours on 32 cores of the cluster. In total, it took about 50 modules. Memory required less than 1 GB per core. In the course of calculations, I collected some information about the quantitative characteristics of the solution. In tab. 1 below presents this information.
Table 1 - Comparison of the numbers of Motzkin and the actual number of cuts required for storage in memory
In the first column, the lattice width is m. In the third - the number of words Motzkin length m. The middle column indicates the actual number of cuts, which turn out to be permissible (symmetry is taken into account and the final state is not counted).
If you wish to see the number of Hamiltonian cycles on a square lattice P 2n × P 2n , then the link to this sequence is in the list of sources.
Thanks for attention.
In the article I will show how to use the dynamic profile programming method for solving the problem of counting the number of Hamiltonian cycles on a rectangular grid of size m by n. On Habré there are several articles on the topic of dynamic programming (for example, this one ), but nowhere is this a more complex application of the method. This approach can also be called the transfer matrix method, as you like.
I warn you that the article contains about 2000 words (8 A4 pages), but the road will be by walking.
')
Summary
- A bit about intractable tasks
- Definitions and problem statement
- Cuts and State Machine
- Matrix transfer method
- Solution without a matrix
- Algorithm complexity
- Modular arithmetic
- Discussions and results
- List of used sources
1. A bit about intractable tasks
What is intractable problem? This is a task that does not have an effective solution algorithm. Moreover, this is not necessarily a problem with an exponential complexity of the solution, the complexity can be polynomial, but with a sufficiently large degree of polynomial (for example, the problem of k queens, which I already wrote about here ). You can learn more about such tasks and their classification in the classic book by M. Gary, D. Johnson “Computing Machines and Intractable Problems”.
Such problems are usually solved by brute force, dynamic programming and combinatorial analysis methods. Often, an acceptable solution is obtained by using these three components at the same time, but this also requires the experience of writing a sufficiently optimal code. It’s very good if you have a cluster of at least several thousand cores and at least a couple of hundred gigabytes of RAM. Unfortunately, I'm not kidding, many tasks can be solved only on such a machine ...
I like to solve intractable problems and I even organize contests for programmers-mathematicians on this topic from time to time. This article is partially confined to the “ Pre-Hamilton cycles ” competition, which began on October 1 and ends on October 31, 2010. The problem proposed in the conditions of the competition is solved by me using the same method (with minor changes), which will be described here.
In the section with the conclusion of the complexity of the algorithm, it is assumed that the reader knows the elements of combinatorics (what is the number of combinations, for example), and in the section about the finite state machine the reader will be forced to recall elements of graph theory (for example, what is the adjacency matrix of the graph, and what does power).
2. Definitions and problem statement
In the work there is a graph, called a rectangular lattice P m × P n . A rectangular lattice is an integer point of the coordinate plane, connected by the principle of the nearest neighborhood. The designation P m × P n is related to the fact that the integer rectangle is the direct product of two chains, the first of which has m links (denoted by P m ), and the second one - n (denoted by P n ). The number m is the width of the lattice (length from left to right), and n is its length (length from bottom to top).
A Hamiltonian cycle in a graph is a cycle that passes through each of its vertices exactly once. In fig. Figure 1 shows an example of a Hamiltonian cycle on a P 6 × P 8 lattice.

Figure 1 - Example of a Hamiltonian cycle on a 6 × 8 grid
The task is to find the number of Hamiltonian cycles on the lattice P m × P n for given m, n ≥ 2. For example, the following figure shows all 6 Hamiltonian cycles on a 4 × 4 grid.

Figure 2 - All 6 Hamiltonian cycles on a 4 × 4 grid
3. Cuts and State Machine
Any cycle in the P m × P n graph can be built sequentially along the “layers” of P m × P k (k = 0,1,2, ..., n). For clarity, in Fig. 3 shows a line cutting the graph into two parts. Below it, the graph P 6 × P 5 , on which the still unfinished “cycle” is a set of disjoint simple chains. This constructed part of the cycle will be called the "past." At the top of the line, one of the possible options for the completion of an unfinished “cycle” (this is the “future”) is depicted. The cycle is closed and does not touch the cut line at its points of inflection. And since, bypassing the cycle in any direction, we will return to the starting point, the cut line will be intersected by the cycle an even number of times.

Figure 3 - Cycle section
The intersection of the cycle by the cut line itself can be represented as a regular bracket sequence, discharged with zeros. For example, in fig. 3 such a sequence has the form (0000) . In this sequence, a pair of matching opening and closing brackets correspond to the two ends of the same chain through the “past”, and the zeros mean that at these points there is no intersection of the cut line with the cycle. Thus, any section can be encrypted with the correct bracket sequence discharged with zeros. Since the initial and final cuts must be zero (consisting entirely of zeros), we must distinguish them, denoting one with a line below, and the second with a line above.
In the process of building a cycle, we do not need to know either the "past" or the "future", but it is enough to store only information about which section at a given time has turned out, and how the rest can be obtained from this section. Indeed, how to move from the current cut to the next? For example, as in fig. 3 is the transition from the cut (0000) to the next cut 00 () 00 ? This will be shown in the examples.

Figure 4 - Examples of the transition from one section to another
In fig. 4 shows 3 examples of transitions from one section to another. The arcuate lines show that the ends of the corresponding vertical arcs are connected through the “past”. The first case shows the transition to fig. 3 The remaining two cases are slightly more complex, but they clearly demonstrate what new cuts can be obtained by adding different combinations of horizontal arcs.
However, not all combinations of horizontal arcs can lead to a new cut. Some combinations may be unacceptable for three reasons, indicated in Figure 5.

Figure 5 - Examples of invalid transitions. Three possible cases
In the first case, one of the three chains closes ahead of time, so the Hamiltonian cycle cannot turn out. In the second case, three arcs meet at the same vertex. Finally, the third case is impossible due to the fact that some vertices were unused (and the Hamiltonian cycle must go through all the vertices).
So, suppose that we have information about all possible sections of our lattice and which sections from which can be obtained by including horizontal arcs. All this information can be represented in the form of a finite automaton whose nodes will be cuts, and the arcs will show the possibility of a transition. In fig. 6 shows an example of such a finite automaton constructed for a 3 × n lattice.

Figure 6 - State machine for the 3 × n grid
The answer to the question of how many cycles exist on the P 3 × P n grid will be the number of ways to go from the initial state of the automaton to the final state in n steps. How to do it? I know two ways: bad and better. I'll start with the bad.
4. The matrix transfer method
One of the ways to solve the problem is called the transfer matrix method, which consists in the following. Let us enumerate all possible cuts from 1 to N in any way, but so that the initial state is number 1 and the final state is number N. We construct a matrix T in which the numbers T ij will be equal to the number of ways to get from the cut i number cut j . The solution of the problem for the lattice P m × P n is the number (T n ) 1, N.
For example, for the P 3 × P n lattice, we have already constructed an automaton (Fig. 6), so we can write out the transfer matrix.

Figure 7 - Transfer matrix, or adjacency matrix of the finite automaton of fig. 6 and her sixth degree
In fig. 7 shows the transfer matrix T for Hamiltonian cycles on the P 3 × P n lattice. The solution will be the number (T n ) 15 . For example, (T 6 ) 15 = 4, so is the number of Hamiltonian cycles on the P 3 × P 6 lattice.
However, in practice this method of solving the problem is applicable, at most, for m = 12, when the transfer matrix for Hamiltonian cycles on the lattice has a size of 3774 × 3774 (see Table 1 in the discussion section) and fits in the RAM of a personal computer. Long numbers are stored in the matrix itself, since, for example, the answer for the P 12 × P 20 grid contains 33 digits, and for the P 12 × P 100 grid, the number of digits reaches 174.
In the section “Modular arithmetic” it will be shown how to get rid of long numbers, sacrificing the speed of calculations, but it still will not save from the monstrous growth of the transfer matrix. Therefore, I called this method of solving the problem bad.
5. Solution without a matrix
This solution, as it is not strange, is also called the transfer matrix method, but the matrix clearly does not appear in it, therefore, this method is called in the Russian-language literature a method of dynamic programming [on a finite state machine].
The meaning of the method is to store the number of ways to get to each vertex of the finite state machine in k steps. At step k = 0, this number is 0 in all vertices except the starting one. The number of ways to be at the starting vertex at step k = 0 is, by definition, set to 1. Let at some step k at vertex i you can be P ways, then going to step k + 1 we add the number P to the number of ways it is at all vertices j, which can be reached from i. But for this you need to know which vertices you can get from i, that is, to store the matrix again! In fact, it is not necessary: getting to vertex i, and knowing what section it denotes, we re- build all such cuts that can come out of it.
How this is implemented in the program is an individual matter. I will explain my approach. Suppose there is a queue Q in which cuts are stored (as a bracket sequence) and the number of ways to be in them. At the beginning of the algorithm, a section consisting of zeros and a number of methods equal to 1 is stored in the queue. Along with the queue, there is a hash table that also stores sections and the number of ways to be in them. At the beginning of the algorithm, the table is empty.
At step k, we get another section i from the queue, and the number of ways P can be in it. We build the set J of all possible cuts obtained from i. For each j of j, we check if it is in the hash table. If not, add j to the table along with the number of methods P. If yes, then from the table we take the number of ways Q that can come in j and write the number P + Q in its place. The exception is the case when j is equal to the zero cut, which means that we got to the final state and have to add the number P to the answer, but not add the zero cut to the hash.
At the end of step k, the queue is empty, so move the data from the hash table to the queue, clear the hash, and go to step k + 1.
I am using a hash with open addressing and double hashing. The number of collisions is 0.6 per call. That is, in 60% of cases, one step is taken on the table, and in other cases it falls right away. I think this is a good hash for such a task.
6. The complexity of the algorithm
First, I will point out the upper limit of complexity, and then I will show what actually happens in practice.
The set of all regular bracket sequences discharged with zeros and having length m are Motzkin words of length m over the alphabet { 0 , ( , ) }, generated by context-free grammar
Z → Y | Y ( Z ) Z,
Y → ε | 0 Y,
where ε denotes an empty word. The number of such words can be calculated from combinatorial considerations:

In this formula, k is the number of pairs of brackets. The first expression under the sum sign (the fraction and the very first binomial coefficient) is the Catalan number , which shows the number of regular bracket sequences, and the second binomial coefficient is the number of ways to put 2k brackets in m positions (filling the remaining positions with zeros).
Thus, the number of all possible cuts for Hamiltonian cycles on the lattice, at least, does not exceed the number of Motzkin words, and Motzkin words grow at a speed of almost 3 m . In fact, such cuts are much smaller, since some may be unacceptable. For example, cuts such as (0) 000 or (() 0) 0 will be unacceptable for a lattice of width 6, since they cannot be obtained when constructing a Hamiltonian cycle. The discussion section will show the table. 1, which indicates the total number of cuts for some m. In reality, it turns out that only a third of Motzkin's words are permissible, and taking into account symmetry, it is enough to store only one fifth of them.
I will explain. Some cuts are palindromes and coincide with themselves with symmetric reflection, but those that are symmetrical to each other can be stored as one section. For example, the cut (()) () and () (()) can be considered one and the same. With this in mind, it turns out that, on average, only one-fifth of Motzkin's words should be stored in the program.
For each section, we have to go through 2 m-1 ways to put horizontal arcs. And all this together we have to do n times.
Total, the algorithm has complexity O (6 m · m -1/2 · n). And in fact, due to the fact that many cuts are unacceptable, in practice the complexity of the algorithm is O (5 m · n). This happened during my observation of the algorithm.
As for the memory used, the main part of the resources is occupied by the queue and the hash table. Each section for m≤32 can be stored in a 64-bit integer, since 2 bits are required for storing brackets and the number 0. Plus a long arithmetic that eats up all the resources completely. But there is one technique that allows you to slow down the calculations, giving up long arithmetic.
7. Modular arithmetic
Let's calculate the answer modulo various primes: 2 31 -1 = 2147483647, 2147483629, 2147483587, ... To do this, the program must be run as many times as we can choose different modules (although, of course, you can count on 2-3 modules at once, in memory). According to the Chinese remainder theorem, it is possible to recover the answer up to the product of all primes used. If the product of all primes is greater than the answer to the problem, then the answer is uniquely restored. How to choose the required number of modules?
For example, let's count the number of cycles on a 16-n grid on two modules. Let n = 1,2, ..., 16. Then get the answers
[0, 1, 128, 405688, 24980352, 776813457, 729683652, 1087605227, 2000673777, 456710131, 1550214608, 568568229, 2047094091, 1175631455, 380271385, 1536681549] (mod 2147483647).
[0, 1, 128, 405688, 24980352, 776813727, 729709644, 1107434405, 301217473, 1373982040, 103268356, 218837622, 1185113726, 2085126539, 1315887233, 2008046410] (mod 2147483629).
According to the Chinese theorem on residues, we have:
[0, 1, 128, 405,688, 24,980,352, 32,989,068,162, 3101696069920, 2365714170297014, 309656520296472068, 2415277789552788286, 3926649012293853406, 726889843182193849, 153366515247378747, 1645735649663585962, 3698490188721496226, 1337259901989820598] (mod · 2147483647 2147483629).
How to check if we have enough 2 modules? In this problem, it is clear that numbers must grow exponentially, which means their logarithms must grow linearly. Take logarithms (for example, natural):
[-INF, 0, 4.852, 12.91, 17.03, 24.22, 28.76, 35.40, 40.27, 42.33, 42.81, 41.13, 39.57, 41.94, 42.75, 41.74].
The logarithm of the product of our two modules is 42.98. We see that the difference between the numbers monotonously grows by about the same amount, and, starting with n = 9, for some reason they stop growing. Moreover, in this place the limit was reached, beyond which the numbers can no longer be. This means that two modules were not enough. Let's take 4 modules and restore the answer:
[0, 1, 128, 405,688, 24,980,352, 32,989,068,162, 3101696069920, 2365714170297014, 309656520296472068, 168435972906750526954, 27738606105535271640888, 12142048779807437697982030, 2344813362310160031818110686, 888511465584607682074513271223, 191678405883294971709423926242394, 65882516522625836326159786165530572] (mod 2147483647 2147483629 · · · 2147483587 2147483579).
Logarithms are:
[-IFN., 0, 4.852, 12.91, 17.03, 24.22, 28.76, 35.40, 40.27, 46.57, 51.68, 57.76, 63.02, 68.96, 74.33, 80.17].
The numbers strictly increase, increasing by about the same amount. The logarithm of the product of 4 selected modules is 85.95, which is noticeably more than the last number in the sequence. That means the answer is correct. You can verify this by typing the query "65882516522625836326159786165530572" in Google.
8. Discussions and results
With this algorithm, I was able to calculate the number of cycles on a 22 × 100 grid. Calculations on a single module lasted about 30 hours on 32 cores of the cluster. In total, it took about 50 modules. Memory required less than 1 GB per core. In the course of calculations, I collected some information about the quantitative characteristics of the solution. In tab. 1 below presents this information.
| m | The real number of cuts | The number of words Motzkin |
|---|---|---|
| 3 | 3 | four |
| four | 6 | 9 |
| five | 12 | 21 |
| 6 | 23 | 51 |
| 7 | 62 | 127 |
| eight | 109 | 323 |
| 9 | 365 | 835 |
| ten | 607 | 2188 |
| eleven | 2355 | 5798 |
| 12 | 3774 | 15511 |
| 13 | 16020 | 41835 |
| 14 | 25188 | 113634 |
| 15 | 113198 | 310572 |
| sixteen | 176061 | 853467 |
| 17 | 821923 | 2356779 |
| 18 | 1270562 | 6536382 |
| nineteen | 6097041 | 18199284 |
| ten | 9387784 | 50852019 |
| 21 | 46013564 | 142547559 |
| 22 | 70652188 | 400763223 |
Table 1 - Comparison of the numbers of Motzkin and the actual number of cuts required for storage in memory
In the first column, the lattice width is m. In the third - the number of words Motzkin length m. The middle column indicates the actual number of cuts, which turn out to be permissible (symmetry is taken into account and the final state is not counted).
If you wish to see the number of Hamiltonian cycles on a square lattice P 2n × P 2n , then the link to this sequence is in the list of sources.
9. List of sources used
- M. Gary, D. Johnson. Computers and inaccessible tasks.
- A003763 - Number of Hamiltonian cycles on 2n X 2n square grid of points.
- The Chinese remainder theorem .
- Catalan numbers , derivation of formulas and asymptotics.
Thanks for attention.
Source: https://habr.com/ru/post/105705/
All Articles