Particle swarm algorithm

Introduction

A flock of birds is a great example of the collective behavior of animals. Flying in large groups, they almost never collide in the air. The pack moves smoothly and in a coordinated way, as if someone controls it. And anyone who hung a bird feeder in his yard knows that after a few hours all the birds in the area will find him.



The point here is not about the leader giving orders - in flocks of many species of birds it is simply not there. Like an ant or bee colony, a flock is a swarm of intelligence. Birds in it act according to certain - quite simple - rules. Circling in the sky, each bird watches its kindred and coordinates its movement according to their position. And having found a food source, she will inform them about it.

The last fact should be discussed in more detail, since it plays one of the key roles in the considered optimization method. The reasons for this “altruism” of birds (and other animals acting in a similar way) have been the subject of study by many sociobiologists. One of the most popular explanations for this phenomenon is that the advantages of each individual flock of such behavior are greater than such obvious disadvantages as the need to fight for food found with other individuals.
')
Food sources are usually located randomly, so alone the bird may well die without finding one for a long time. However, if all birds “play by the rules”, sharing information about the finds with their relatives, then the chances of each of them for survival are sharply increased. Thus, being ineffective for an individual, such a strategy is the key to the effectiveness of the pack and the species as a whole.

Boids

Bird watching inspired Craig Reynolds to create a computer model in 1986, which he called the Boids. To simulate the behavior of a flock of birds, Reynolds programmed the behavior of each of them individually, as well as their interaction. However, he used three simple principles. First, each bird in its model sought to avoid collisions with other birds. Secondly, each bird moved in the same direction as the nearby birds. Third, the birds sought to move at the same distance from each other.

The results of the first simulations surprised the creator himself: despite the simplicity of the algorithms underlying the program, the pack looked extremely plausible on the screen. The birds were knocked down in groups, escaped from collisions, and even randomly rushed about like real ones.
As an expert in computer graphics, Craig Reynolds was primarily interested in the visual side of the results of the simulation created by him. However, in the article devoted to Boids, he also noted that the behavioral model developed by him can be expanded by introducing additional factors, such as the search for food or the fear of predators [1].

Classic particle swarm algorithm

In 1995, James Kennedy (James Kennedy) and Russell Eberhart (Russel Eberhart) proposed a method for optimizing continuous nonlinear functions, which they called the particle-swarming algorithm [2]. They were inspired by the Reynolds simulation model, as well as the work of Heppner and Grenader on a similar theme [4]. Kennedy and Eberhart noted that both models are based on controlling the distances between birds - and, therefore, the synchronism of the pack is a function of the efforts that the birds make to maintain the optimal distance.

The algorithm developed by them is quite simple and can be implemented in literally several dozen lines of code in any high-level programming language. He models a multi-agent system, where particle agents move to optimal solutions, sharing information with their neighbors.

The current state of a particle is characterized by coordinates in the solution space (that is, the solution associated with them), as well as by the displacement velocity vector. Both of these parameters are randomly selected at the initialization stage. In addition, each particle stores the coordinates of the best solutions found by it, as well as the best solutions passed by all particles - this simulates the instantaneous exchange of information between birds.

At each iteration of the algorithm, the direction and length of the velocity vector of each of the particles change in accordance with information about the optimum found:

,

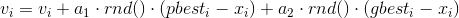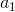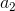Where - particle velocity vector ( - its i-th component), , - constant acceleration 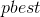- the best point found by a particle 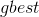- the best point passed by all particles of the system, 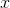- the current position of the particle, and the function 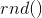returns a random number between 0 and 1, inclusive.

After calculating the direction of the vector the particle moves to a point . If necessary, the values ​​of the best points for each particle and for all particles as a whole are updated. After that the cycle repeats.

Modifications of the classic algorithm

The particle swarm algorithm has appeared relatively recently, but various researchers have already proposed a number of its modifications, and new works on this subject do not cease to be published. There are several ways to improve the classical algorithm, implemented in most of them. This combination of the algorithm with other optimization algorithms, reducing the likelihood of premature convergence by changing the characteristics of particle motion, as well as dynamically changing the parameters of the algorithm during optimization. Below are the most notable of the modifications.

Lbest

Later in 1995, an article by Kennedy and Eberhart was published, in which they named the original algorithm “GBEST”, because it uses the global best solution (global best) to form the velocity vectors, and also proposed its modification, which they called “LBEST”. When updating the direction and velocity of a particle in LBEST, they use information about the solutions of neighboring particles:

,

Where 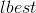- the best result among the particle and its neighbors. Neighboring are considered to be either particles that differ from this index by no more than a certain specified value, or particles whose distance does not exceed a given threshold.

This algorithm explores the search space more thoroughly, but is slower than the original one. Moreover, the fewer the number of neighbors taken into account when forming the velocity vector, the lower the rate of convergence of the algorithm, but the more efficiently it avoids suboptimal solutions.

Inertia Weighted PSO

In 1998, Yuhui Shi and Russell Eberhart proposed a modification that, at first glance, is only slightly different from the classical algorithm [5]. In their article, Shi and Eberhart noted that one of the main problems in solving optimization problems is the balance between careful research of the search space and the rate of convergence of the algorithm. Depending on the task and the characteristics of the search space in it, this balance should be different.
With this in mind, Shea and Eberhart proposed to change the rule for updating the particle velocity vectors:

,

Coefficient 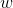, they called the coefficient of inertia, determines the mentioned balance between the breadth of the study and attention to the found suboptimal solutions. In the case when , the speeds of particles increase, they fly apart and explore space more carefully. Otherwise, the particle velocities decrease with time, and in this case the rate of convergence depends on the choice of parameters 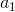and .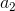

Time-Varying Inertia Weighted PSO

In their 1998 paper, Shi and Eberhart noted that inertia does not have to be a positive constant: it can change during the operation of the algorithm according to a linear and even non-linear law [5]. In an article in 1999 and later papers, they most often used the linear law of decreasing, as quite effective and at the same time simple [6]. However, other laws of inertia change were developed and successfully applied.

The value of the coefficient of inertia can both decrease and grow. When it decreases, the particles first explore the search field extensively, finding many suboptimal solutions, and over time more and more concentrate on the study of their surroundings. The increase in inertia contributes to the convergence of the algorithm in the later stages of work.

Canonical PSO

In 2002, Maurice Clerc and James Kennedy proposed their own modification of the particle swarm algorithm, which has become so popular that it is now called the canonical particle swarm algorithm [7]. It allows you to get rid of the need to "guess" the appropriate values ​​of the adjustable parameters of the algorithm, controlling the convergence of particles.

Claire and Kennedy changed the way they calculated the velocity vectors of particles by introducing an additional factor into it:

,

Where 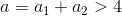and compression ratio 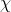equals:

.

This approach ensures the convergence of the algorithm without the need to explicitly control the speed of the particles.

Fully Informed Particle Swarm

In their 2004 paper, Rui Mendes, James Kennedy, and José Neves noted that the assumption adopted by the canonical particle-digging algorithm that only the most successful affects each of the particles does not correspond to its underlying natural mechanisms and, possibly, leads to a decrease in the efficiency of the algorithm [8]. They suggested that due to the excessive attention of the algorithm to a single solution, important information about the structure of the search space may be lost.

Based on this, they decided to make all particles “fully informed”, that is, receive information from all neighboring particles. To do this, they changed in the canonical algorithm the law of change of speed:

,

Where 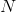- many neighbors of a particle, 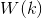- the best of the points passed by the k-th neighbor. - a weight function that can reflect any characteristic of the k-th particle that is considered important: the value of the objective function at the point at which it is located, the distance from it to a given particle, and so on.

Conclusion

In the first article describing the particle swarm algorithm, James Kennedy and Russell Eberhart expressed the idea of ​​using an algorithm to imitate social behavior — Kennedy, as a social psychologist, was extremely attracted to this idea [1]. However, the algorithm was most widely used in optimization problems for complex multidimensional nonlinear functions.

The particle swarm algorithm is widely used, among others, in machine learning tasks (in particular, for training neural networks and image recognition), parametric and structural optimization (shapes, sizes and topologies) in the field of design, in the fields of biochemistry and biomechanics. In terms of efficiency, it can compete with other methods of global optimization, and low algorithmic complexity contributes to the simplicity of its implementation.

The most promising areas for further research in this direction should be theoretical studies of the causes of convergence of the particle swarm algorithm and related issues from the fields of swarm intelligence and chaos theory, combining various modifications of the algorithm to solve complex problems, considering the particle swarming algorithm as a multi-agent computing system, and study of the possibilities of including in it analogues of more complex natural mechanisms.

Literature

[1] Craig Reynolds, “Flocks, Herds, and Schools: A Distributed Behavioral Model” // Computer Graphics, 21 (4), pp. 25–34, 1987
[2] J. Kennedy, RC Eberhart, “Particle swarm optimization” // In Proceedings of the IEEE International Conference on Neural Networks, pp. 1942–1948, 1995
[3] RC Eberhart, J. Kennedy, “A new optimizer using particle theory” // Proceedings of the Sixth International Microscope, pp. 39–43, 1995
[4] F. Heppner, U. Grenander, “A stochastic nonlinear model for coordinated bird flocks” // The Ubiquity of Chaos, pp. 233–238, 1990
[5] Y. Shi, R. Eberhart, “A modified particle swarm optimizer” // The 1998 IEEE International Conference on Evolution Computation Proceedings, pp. 69–73, 1998.
[6] Y. Shi, R. Eberhart, “Empirical study of particle swarm optimization” // Proceedings of the 1999 IEEE Congress on Evolutionary Computation, p. 1945–1950, 1999.
[7] M. Clerc, J. Kennedy, “The Multidimensional Complex Space,” IEEE Transactions on Evolutionary Computation, No. 6 (1), pp. 58–73, 2002 .
[8] R. Mendes, J. Kennedy, J. Neves, “The fully informed particle swarm: Simpler, maybe better” // IEEE Transactions on Evolutionary Computation, No. 8 (3), pp. 204–210, 2004