Ant algorithms
Foreword
Most recently, this blog has published an article on the behavior of a swarm of bees. This article talks about a different swarm intelligence algorithm called the ant algorithm . It consists of an introduction briefly telling about the borrowed natural mechanism, a description of the original Marco Dorigo algorithm, a review of other ant algorithms, and a conclusion that indicates the areas of application of ant algorithms and promising directions in their research.
Introduction
An ant cannot be called savvy. A single ant is not able to make the slightest decision. The fact is that it is arranged extremely primitive: all its actions are reduced to elementary reactions to the environment and their fellows. The ant is not able to analyze, draw conclusions and look for solutions.
These facts, however, do not agree with the success of ants as a species. They exist on the planet for more than 100 million years, build huge dwellings, provide them with everything they need and even lead real wars. In comparison with the complete helplessness of individuals, the achievements of ants seem unthinkable.
Ants can achieve such success due to their sociality. They live only in collectives - colonies. All ants of the colony form the so-called swarm intelligence . The individuals that make up the colony do not have to be smart: they must only interact according to certain — extremely simple — rules, and then the colony will be entirely effective.
')
There are no dominant individuals in the colony, no bosses or subordinates, no leaders who distribute instructions and coordinate actions. The colony is completely self-organizing. Each of the ants has information only about the local situation, not one of them has any idea about the whole situation - only about what he learned himself or from his relatives, explicitly or implicitly. The implicit interactions of ants, called stigmergy , are based on mechanisms for finding the shortest path from an anthill to a food source.
Each time passing from the anthill to food and back, the ants leave behind a path of pheromones. Other ants, feeling such traces on the ground, will instinctively rush to it. Since these ants also leave pheromone paths behind them, the more ants go along a certain path, the more attractive it becomes for their relatives. At the same time, the shorter the path to the food source, the less time it takes for the ants to get on it - and therefore, the faster the traces left on it become noticeable.
In 1992, in his dissertation, Marco Dorigo (Marco Dorigo) proposed to borrow the described natural mechanism for solving optimization problems [1]. Imitating the behavior of an ant colony in nature, ant algorithms use multi-agent systems, the agents of which operate according to extremely simple rules. They are extremely effective in solving complex combinatorial problems, such as, for example, the traveling salesman problem, the first to be solved using this type of algorithm.
The classic ant algorithm for solving the traveling salesman problem
As mentioned above, the ant algorithm simulates a multi-agent system. We will call its agents ants later. Like real ants, they are fairly simple: they need a small amount of memory to perform their duties, and they do simple calculations at every step.
Each ant keeps in memory a list of nodes it has passed. This list is called the tabu list or simply the memory of an ant. Choosing a node for the next step, the ant “remembers” about the nodes that have already been passed and does not consider them as possible for the transition. At each step, the list of prohibitions is replenished with a new node, and before the new iteration of the algorithm — that is, before the ant passes the path again — it is empty.
In addition to the list of prohibitions, when choosing a node for the transition, the ant is guided by the “attractiveness” of the ribs that it can pass. It depends, firstly, on the distance between the nodes (that is, on the weight of the edge), and secondly, on the traces of pheromones left on the edge by ants that passed along it. Naturally, unlike rib weights, which are constant, traces of pheromones are updated at each iteration of the algorithm: as in nature, traces evaporate over time, and passing ants, on the contrary, strengthen them.
Let the ant be in the node
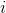 and node
and node 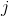 - this is one of the nodes available for transition:
- this is one of the nodes available for transition:  . Denote the weight of the edge connecting the nodes.
. Denote the weight of the edge connecting the nodes. 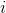 and
and 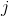 , as
, as  and the pheromone intensity on it is like
and the pheromone intensity on it is like 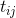 . Then the probability of an ant moving from
. Then the probability of an ant moving from 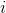 at
at 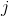 will be equal to:
will be equal to: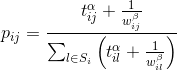
Where
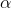 and
and 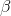 - these are adjustable parameters that determine the importance of the components (edge weight and pheromone level) when choosing a path. Obviously, when
- these are adjustable parameters that determine the importance of the components (edge weight and pheromone level) when choosing a path. Obviously, when  the algorithm turns into a classic greedy algorithm, and when
the algorithm turns into a classic greedy algorithm, and when  he will quickly come to some sub-optimal solution. The choice of the correct ratio of parameters is the subject of research, and in general is based on experience.
he will quickly come to some sub-optimal solution. The choice of the correct ratio of parameters is the subject of research, and in general is based on experience.After the ant successfully passes the route, it leaves a trace on all the ribs inversely proportional to the length of the path:
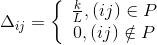 ,
,Where
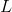 - path length, and
- path length, and 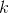 - adjustable parameter. In addition, traces of pheromone evaporate, that is, the intensity of the pheromone on all edges decreases at each iteration of the algorithm. Thus, at the end of each iteration, it is necessary to update the intensity values:
- adjustable parameter. In addition, traces of pheromone evaporate, that is, the intensity of the pheromone on all edges decreases at each iteration of the algorithm. Thus, at the end of each iteration, it is necessary to update the intensity values:\cdot t_{ij} +\Delta t_{ij})
Review of modifications of the classical algorithm
The results of the first experiments with the use of the formic algorithm for solving the traveling salesman problem were promising, but far from being the best as compared to the methods that already existed. However, the simplicity of the classical ant algorithm (called the "ant system") left room for improvement — and it was the algorithmic improvements that were the subject of further research by Marco Dorigo and other specialists in the field of combinatorial optimization. Basically, these improvements are associated with greater use of the search history and a more thorough study of the areas around the already found successful solutions. Below are the most notable of the modifications.
Elitist Ant System
One of these improvements is the introduction of so-called "elite ants" into the algorithm. Experience has shown that when passing edges that are included in shorter paths, ants are more likely to find shorter paths. Thus, an effective strategy is to artificially increase the level of pheromones on the most successful routes. To do this, at each iteration of the algorithm, each of the elite ants follows a path that is the shortest one found at the moment.
Experiments show that, up to a certain level, increasing the number of elite ants is quite effective, allowing you to significantly reduce the number of iterations of the algorithm. However, if the number of elite ants is too large, then the algorithm quickly finds a suboptimal solution and gets stuck in it [3]. Like other variable parameters, the optimal number of elite ants should be determined empirically.
Ant-Q
Luca M. Gambardella and Marco Dorigo published a paper in 1995 in which they presented an ant algorithm, which was named after the Q-learning machine learning method [4]. The algorithm is based on the idea that the ant system can be interpreted as a learning system with reinforcement. Ant-Q reinforces this analogy by borrowing many ideas from Q-learning.
The algorithm stores a Q-table that associates with each of the edges a value that determines the “utility” of the transition along this edge. This table is changed during the operation of the algorithm - that is, the training system. The value of the transition utility over the edge is calculated based on the values of the transition utilities along the following edges as a result of the preliminary determination of possible next states. After each iteration, the utilities are updated based on the lengths of the paths that included the corresponding edges.
Ant Colony System
In 1997, the same researchers published a paper on another ant algorithm developed by them [5]. To improve efficiency compared to the classical algorithm, they introduced three major changes.
First, the level of pheromones on the edges is updated not only at the end of the next iteration, but also at each transition of ants from node to node. Secondly, at the end of the iteration, the pheromone level rises only on the shortest of the found paths. Thirdly, the algorithm uses a modified transition rule: either, with a certain probability, the ant certainly chooses the best - according to the length and level of pheromones - an edge, or makes a choice in the same way as in the classical algorithm.
Max-min Ant System
In the same year, Thomas Stützle (Tomas Stützle) and Holger Hoos (Holger Hoos) proposed an ant algorithm in which the increase in the concentration of pheromones occurs only on the best paths of the ants passed [6]. Such great attention to local optima is compensated by the introduction of restrictions on the maximum and minimum concentration of pheromones on the ribs, which very effectively protect the algorithm from premature convergence to suboptimal solutions.
At the initialization stage, the concentration of pheromones on all edges is set equal to the maximum. After each iteration of the algorithm, only one ant leaves a trace - either the most successful at this iteration, or, similarly to the algorithm with elitism, elite. This achieves, on the one hand, a more thorough study of the search area, on the other - its acceleration.
Asrank
Bernd Bulnheimer, Richard Hartl and Christine Strauß developed a modification of the classical ant algorithm, in which at the end of each iteration the ants are ranked according to the length of the paths they traveled [7]. The number of pheromones left by an ant on the ribs is, therefore, assigned in proportion to its position. In addition, the algorithm uses elite ants to more thoroughly explore the surroundings of successful solutions already found.
Conclusion
The traveling salesman problem is perhaps the most researched combinatorial optimization problem. It is not surprising that it was she who was chosen first to be solved using an approach borrowing the mechanisms of ant colony behavior. Later, this approach found application in solving many other combinatorial problems, including assignment problems, graph coloring tasks, routing problems, data mining and image recognition, and others.
The effectiveness of ant algorithms is comparable with the efficiency of general meta-heuristic methods, and in some cases with problem-oriented methods. The best results are shown by ant algorithms for problems with large dimensions of the search domains. Ant algorithms are well suited for use with local search procedures, allowing you to quickly find the starting points for them.
The most promising areas for further research in this area should be considered as an analysis of the method for selecting custom parameters of algorithms. In recent years, various methods have been proposed for adapting the parameters of algorithms on the fly [8]. Since the behavior of ant algorithms strongly depends on the choice of parameters, it is this problem that attracts the most attention of researchers at the moment.
Literature
[1] M. Dorigo, “Ottimizzizzazione, apprendimento automatico, ed algoritmi basati su metafora naturale (Optimization, Learning, and Natural Algorithms)”, thesis for the degree of “Doctorate in Systems and Information Electronic Engineering”, Politecnico di Milano, 1992 year
[2] A. Colorni, M. Dorigo, V. Maniezzo, “Distributed Optimization by Ant Colonies” // Proceedings of the First European Conference on Artificial Life, Paris, France, Elsevier Publishing, pp. 134-142, 1991
[3] M. Dorigo, V. Maniezzo, A. Colorni, “The Ant System: Optimization of Cooperative Agents” // IEEE Transactions on Systems, Man, and Cybernetics-Part B, 26, 1, p. 29 -41, 1996
[4] LM Gambardella, M. Dorigo, “Ant-Q: A Reinforcement Learning Approach to the Traveling Salesman Problem” // Twelfth International Conference on Machine Learning, Morgan Kaufmann, pp. 252-260, 1995
[5] M. Dorigo, LM Gambardella, Ant Colony System: A Cooperative Learning Problem // The IEEE Transactions on Evolutionary Computation Vol. 1, 1, pp. 53-66, 1997
[6] T. Stützle, H. Hoos, “IEEE International Conference on Evolutionary Computation,” p. 309-314, 1997.
[7] Bernd Bullnheimer, Richard F. Hartl, Christine Strains, “A new rank based version of the Ant System.” A computational study ”// Adaptive Information Systems in Economics and Management, 1, 1997
[8] T. Stützle, M. López-Ibáñez, P. Pellegrini, M. Maur, M. de Oca, M. Birattari, Michael Maur, M. Dorigo, “Parameter Adaptation in Ant Colony Optimization” // Technical Report, IRIDIA, Université Libre de Bruxelles, 2010
Source: https://habr.com/ru/post/105302/
All Articles