The principles of the poker bot. part 2
This article is a continuation of this habratopik . In this part of creating a poker bot, we will talk about the decision-making algorithm. Basically, it will focus on strategies that can be successfully applied and receive some kind of income. It is necessary to understand that standard algorithms can work in plus only on small limits, where there are many players with a very non-optimal game who are willing to give us a lot of money. For further improvement, you need to introduce additional elements that players of higher limits take into account using player statistics.
Basics of Poker Mathematics
Poker is in many ways a mathematical game. Especially a large part of the mathematics is in online games, because we do not see our opponent, we cannot use the so-called “telsy” - tips that the player’s behavior gives us. All our decisions are based on the estimated range of the opponent's cards and how our hand stands against this range.
')
To determine the profitability of an action, we use the concept of mathematical expectation in monetary terms, or EV (Expected Value). It is defined as the sum of all possible outcomes of an event expressed in money multiplied by the probability of this event:
EV = X 1 ($) * P X1 + X 2 ($) * P X2 +… + X n ($) * P Xn .
For example, let's take a situation: a no-limit hold'em game with blinds of $ 1 / $ 2, we have Q in our hands
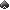Q 
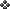and $ 200 per stack, opponent A has 
K and $ 200. Suppose the following actions occur preflop: you are raised to $ 8 in the small blind (everyone folds to you), your opponent in the big blind still raises to $ 20. We have 3 possible actions: fold (fold), call (call), raise (raise). For simplicity, we assume that we will do the following increase for the whole stack, the so-called push. Calculate the EV of each of the actions.
EV fold is always zero.
To calculate EV, Eq. We take the following assumptions: if the flop is A or K, then we immediately play check / fold; if not, then we play a check, our opponent bets (let it be $ 25), we raise and our opponent folds. We get two events and the probability of A or K going to the flop is 32%.
EV equal = ($ 40 - $ 12 + $ 25) * 0.68 + (-12 $) * 0.32 = $ 32.2.
To calculate the EV push, we assume that the opponent is always ready to play the stack. To determine the probability of the outcome of each of the events, use the wonderful program PokerStove (you can download it here ). The principle of its work is quite simple: considering the given cards (specific or card ranges) of opponents, the program randomly distributes the missing cards of the board a large number of times, and thus the probability of winning / draw for each opponent in percentages is statistically obtained. In our case, the probability of winning 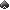Q
Q 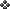- 53.786% and 46.214% for A K . Get the EV calculation:
Push Push EV = $ 208 * 0.53786 + (-192 $) * 0.46214 = $ 28.9.
As a result, we have a positive EV for both calling and pushing. Moreover, a call is more profitable, because on average, each time $ 32.2 will be paid to us. We received a rather simplified calculation based on what our opponent's cards knew. In the real game, we will not see the opponent's cards and he may not be alone, which complicates the calculation of EV. For the actions of opponents in the full calculation will be taken into account three actions: fold, call, raise; and for each street. Therefore, the number of terms in the calculation will increase greatly. In addition, we will not be able to accurately determine the probability of an opponent's actions (how often he will raise, call), but in any case, EV is a common parameter for determining the profitability of an action.
For a simple algorithm for playing on micro-limits, it is sufficient to clearly define the rules with which cards are worth playing, and with which are not. First, we will look at the simplest strategies that can be easily algorithmized, and then we will discuss how to improve decision making by the bot with the help of additional parameters and non-standard techniques.
Short Stack Strategy
One of the basic strategies is the Short Stack Strategy (SSS). Its main advantages are that it is quite simple, basically it is an exact algorithm of actions for each of the variants of the rally; the main disadvantage is a small win. In general, the concept of winrate is used to determine the profitability of a game in poker, which is measured in BB / 100 hands - the number of big blinds won per 100 hands. So, for a standard SSS, the average win rate is 2 BB / 100, although the professionals of this strategy, using additional techniques, can bring the profit up to 5 BB / 100 and more. Not so long ago, in the Pokerstars room, the accounts on which the bots played were revealed and they used exactly the strategy of short stacks, details can be read here . In general, it is quite difficult to identify bots, you need to have a very large history of hands on them in order to somehow prove the stereotyped nature of their actions, so it is not known how many bots play on the Internet now.
Briefly consider the strategy itself, a detailed description of it can always be found on poker sites. Its very name comes from the fact that you need to enter the game with a short stack. The standard purchase of No Limit Hold'em is 100 BB, for SSS you need to enter the game with 20 BB. And if the stack becomes more than 30 BBs, you need to leave the table, because the strategy becomes unprofitable; and if the stack drops to 15 BB, you need to re-buy again to 20 BB. A small stack leads to the fact that often the game ends already on the flop or the maximum on the turn, because after raising preflop we only have all-in or fold on the flop. Therefore, the strategy is very simple and you do not need to take into account all possible options for the development of actions postflop.
The strategy itself is applied at long (full ring) tables (9-10 people), the fewer people at the table, the worse for a short stack, and it is not profitable to play against other short stacks. Therefore, when choosing tables, you need to look at tables with at least 6-7 players with a full stack.
The beginning of our strategy is the starting hands chart (descriptions with which hands it is worth entering the game preflop, when we see only two cards in our hands). We get an exact table of actions preflop:
Where s - suited cards (suited), if the letters "s" are not present, then cards are also suited and unsuited. For example, the range “77+, AJ +, ATs, KQs” includes - “AA, KK, QQ, JJ, TT, 99, 88, 77, AKs, AKo, AQs, AQo, AJs, AJo, ATs, KQs”.
Let's determine the size of the bets: we increase by 4 BB + 1 BB for each limper (limp - calling the game preflop with a call). For example, with BB = 0.1 $ and two limpers in front of us, if we want to enter the game with a raise, we should bet 4 * 0.1 $ + 2 * 0.1 $ = 0.6 $. If there has already been a raise before us and we want to make a re-raise, then its size should be 3 times the size of the raise + 1 raise for each call equalized. For example, with an increase of $ 0.4, we need to bet $ 1.2. There is still a rule: if the size of our bet is more than half of our stack, then you should immediately move all in.
We have analyzed preflop actions, now let's define what we should do with 3 open cards on the table. You need to continue to bet and play, if necessary, on the stack with the finished hand (top pair and better) and strong draws (when one card is not enough to flush or straight). It is also necessary to use the continued bid, but about this technique in the last part of the article.
Recently, there is a tendency to fight poker rooms with short stacks. On Full Tilt, the minimum entry to the game is 35 BB on standard tables and there are a small number of tables where you can play with 20 BBs on the stack, where it is often not profitable to play according to the SSS strategy due to the large number of short stacks at the tables. Pokerstars divided their tables at minimum-maximum purchases by 20-50 BB, 50-100 BB. But all the same, in all rooms there are tables for playing with a short stack, and in smaller poker rooms there are no such restrictions at all where you can successfully use this strategy.
Independent chip model (ICM)
ICM is a mathematical model that is used in Sit-n-go games (CIS) and is successfully used in the late stage of these tournaments, the so-called push-fold. Usually this stage comes when the stack becomes less than 10 BB and there is no sense to enter the game with a raise or a call, and there are only two options for playing: push or fold. In tournaments other than EV (or chipEV, cEV), you need to introduce the concept of $ EV - the cash value of EV (how many chips are in prize money), because in tournaments they do not match. This can be seen quite clearly in the initial stage, when doubling chips (EV) will not double the $ EV. Therefore, there are such border moves that are simultaneously + EV and - $ EV, it is important for us to receive a monetary profit, make moves + $ EV.
Then a small tie-in with boring ICM math, who are not interested, can skip this section.
In ICM, to calculate $ EV - the player's expected income based on the current number of chips, the following method is used: the probability with which the player takes a certain place is calculated, then each of the probabilities is multiplied by the money equivalent for that place and summed up. The probability of winning first place is defined as the ratio of the number of player chips to all chips in a tournament. For clarity, we will use an example: in a CIS tournament for 10 people, costing $ 10 (distribution of prizes between the first 3 places: $ 5, $ 3, $ 2) there are 3 players left with stacks: A = 7500, B = 4500, C = 3000 (for simplicity and clarity of calculations we will not take into account that the blinds have already been put and are not in the stacks of players). Thus, the probability of winning first place for player B:
P B1 = V B / (V ALL ) = 4500 / (7500 + 4500 + 3000) = 30%.
To determine the probability of a player B to take 2nd place, you need to determine it for the case if player A wins (R A1 = 50%) and if player C wins (P C1 = 20%) and add them together. In this case, the winner’s stack is not taken into account:
P B2 = P A1 * P B2, C3 + P C1 * P B2, A3 =
= 0.5 * 4500 / (4500 + 3000) + 0.2 * 4500 / (4500 + 7500) = 0.395 = 39.5%.
We get P B3 = 1 - P B1 - P B2 = 1 - 0.3 - 0.395 = 0.305 = 30.5%.
So $ EV B = P B1 * V1 $ + P B2 * V2 $ + P B3 * V3 $ =
= 0.3 * $ 5 + 0.395 * $ 3 + 0.305 * $ 2 = $ 3.30.
Now that we know how to calculate $ EV, we can determine the profitability of our move. To clarify our example, player B is in the small blind position with A
With a fold, nothing changes and Player B has the same $ EV fold = $ 3.30.
When pushing there are three options:
- 1. Player C will accept our bet and lose. Suppose he calls with a range: 88+, A9s +, ATo, KTs +, KQo (10% of the spectrum), then he loses in 42% of cases. The probability of such an outcome is 10% * 42% = 4.2%, and $ EV B after it will be $ 4.
- 2. Player C will accept our bet and win. The probability of this outcome is 10% * 58% = 5.8%, and $ EV B = $ 2.47.
- 3. Player C will fold 90% of the time and EV B will remain equal to $ 3.30.
We get a total of $ EV push taking into account all possible outcomes:
$ EV push = 0.042 * $ 4 + 0.058 * $ 2.47 + 0.9 * $ 3.295 = $ 3.28. Those. Our share in the tournament after this push will eventually decrease, it turns out to be unprofitable. In fact, the difference is insignificant, so this push can be called borderline, i.e. it is profitable for us to do it with the best hands, but not with the worst. The calculations did not take into account the blinds, so as not to be confused with unnecessary numbers, but the principle of calculation was clear.
If everything is clear with mathematics, then only one relative value remains - the range of cards with which the opponent will answer or raise, which we need to calculate our chances of winning. For this, you can use predefined average call and push ranges for different levels of the stack relative to the blinds. For example, for 9-10 BB, you can take a push range from early position: 77+, AJs, AQo, KQs; and calling: TT +, AQ. The fewer blinds in the stack, the wider the range. Ready-made push-fold tables can be found and used on many poker sites, you can take them for the ranges of the average player. And if you work well with these ranges, you can get quite a positive bot.
Improving Algorithms
The basic algorithms are the basis for an improved strategy, it will be very useful to diversify the game of the bot with the techniques that other players often use and make it possible to confuse the opponent with their actions. In general, let's talk about bluffing, or rather his particular cases.
Continued bet - a bet on the next street with aggression on the previous (raise, re-raise). A very popular trick, often used on the flop if we raise a pre-flop with a good card (for example, AK), but we don’t hit the board and still make a bet, showing that we have a good card (say, a high pair). For a bot, so that its game is not too readable, you can enter a continued bet in 70-80% of cases. The size of the bet must be chosen the same as the bet with the cards in hand so that it is impossible to determine the bluff. For an advanced continuation bet, you can choose the appropriate flops for her. Because the purpose of this technique is to force the opponent to fold, then we need to choose flops in which the opponent is more likely not to hit. Usually this is an uncoordinated offsuit flop, preferably with one high card (so that your opponent does not want to continue the game if he has a pair below), for example A27, K35.
An aggressive draw is a semi-bluff variant when we can get a monster combination on the following streets. It makes sense for a double-sided straight draw (we have QJ, on the table KT4 - ace and 9-ka give us a straight), a flush draw (we have AhTh, on the table 9h5h3c - any chirva gives us a nut flush) . Reception is performed with the expectation that the opponent will fold, and even if the struggle continues, we have a chance to get the best hand. At what our monster will be disguised, because we showed aggression, when there was no possibility of a flush or straight. When programming a bot, you can use this technique, say, in 60-70% of cases.
Disguise - here I would like to mention how you can try to disguise the behavior of our bot. Determining a program based on a sufficient hand history is not so difficult - preflop and postflop actions will give it away. To avoid this, you can enter an element of chance in the choice of cards to be played. For example, if we have a draw of JJ + pairs in the range, then jacks can be played in 80% and, for example, tens in 20% of cases. Or vary call and raise, say 50/50. It is still useful sometimes to play random cards in general (as is often the case with people), then it will not be possible to select the exact range of cards played and determine patterned actions.
Conclusion
We have reviewed the short stack strategy and ICM with you, because they are fairly simple to describe. There is a more general strategy of large stacks for no-limit hold'em, but it includes much more nuances, because the game continues on the turn and on the river, unlike the CCC, and the description will take more than one article. The same can be said about limit hold'em - the strategy of the game cannot be described briefly, but it is even more suitable for algorithmization, because mathematics plays a greater role in it (than in no-limit hold'em). Therefore, with proper knowledge of the strategy in limit hold'em, you can quite successfully apply it to the compilation of the algorithm.
And yet do not forget that the use of bots and any similar programs that give an advantage over other players is prohibited in any poker rooms, so do not take this article as a guide to action.
Article Pokeroff.ru specifically for Habrahabr
Source: https://habr.com/ru/post/105025/
All Articles