Using the Tanimoto coefficient to find people with the same preferences
Solving the exercises for the book “We Program Collective Intelligence”, I decided to share the implementation of one of the algorithms mentioned in this book (Chapter 2 - Exercise 1).
The initial conditions are as follows: suppose we have a dictionary with critique ratings:
The higher the score, the more like the movie.
It is necessary to calculate: how much are the interests of critics similar, for example, so that on the basis of one's ratings one can recommend films to another?
')
Tanimoto coefficient - describes the degree of similarity of two sets. On the Internet, I found several variants of the formula for calculating it. And I decided to dwell on the following:
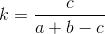
, where k is the Tanimoto coefficient (a number from 0 to 1), the closer it is to 1, the more similar the sets;
a is the number of elements in the first set;
b is the number of elements in the second set;
c is the number of common elements in two sets;
Now we need to compare the estimates of two critics.
Just want to clarify one point. What should be considered a common element in our two sets? It is clear that the presentation of the assessment in the current form will not allow to accurately determine people with similar interests. After all, in essence, the same estimates of 3.5 and 4.0 for this algorithm are completely different numbers. Therefore, in my opinion, the Tanimoto coefficient should be used if the number of rating options is no more than 2-3 (for example, “I liked, did not like” or “I recommend, I didn’t watch, I do not recommend”) applied the following conversion to the estimates: If the score is less than 3, then the film did not like (the score becomes - 0), otherwise - the like (score becomes - 1). Data in this form is more suitable for our experiment.
At the output we get the following dictionary:
And then we write a function that calculates the coefficient of similarity of the estimates of the two critics.
Check the performance of the tanimoto function.
>>> print tanimoto (critics, 'Gene Seymour', 'Lisa Rose')
>>> 0.5
In my opinion, the result is correct. It should be noted that with an increase in the number of assessments for each critic, the accuracy of calculating the similarity coefficient will increase.
If we had a database of estimates, it would be possible to calculate the coefficients of the similarity of interests of people and begin to make recommendations using the Tanimoto method.
Download the sample text here .
Download the full text of all examples from the book on the author's website . You can also find a more complete array with critics.
The initial conditions are as follows: suppose we have a dictionary with critique ratings:
critics = { 'Lisa Rose' : { 'Superman Returns' : 3.5 , 'You, Me and Dupree' : 2.5 , 'The Night Listener' : 3.0 } ,
'Gene Seymour' : { 'Superman Returns' : 5.0 , 'The Night Listener' : 3.5 , 'You, Me and Dupree' : 3.5 } }
The higher the score, the more like the movie.
It is necessary to calculate: how much are the interests of critics similar, for example, so that on the basis of one's ratings one can recommend films to another?
')
Tanimoto coefficient - describes the degree of similarity of two sets. On the Internet, I found several variants of the formula for calculating it. And I decided to dwell on the following:
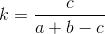
, where k is the Tanimoto coefficient (a number from 0 to 1), the closer it is to 1, the more similar the sets;
a is the number of elements in the first set;
b is the number of elements in the second set;
c is the number of common elements in two sets;
Now we need to compare the estimates of two critics.
Just want to clarify one point. What should be considered a common element in our two sets? It is clear that the presentation of the assessment in the current form will not allow to accurately determine people with similar interests. After all, in essence, the same estimates of 3.5 and 4.0 for this algorithm are completely different numbers. Therefore, in my opinion, the Tanimoto coefficient should be used if the number of rating options is no more than 2-3 (for example, “I liked, did not like” or “I recommend, I didn’t watch, I do not recommend”) applied the following conversion to the estimates: If the score is less than 3, then the film did not like (the score becomes - 0), otherwise - the like (score becomes - 1). Data in this form is more suitable for our experiment.
def prepare_for_tanimoto ( critics_arr ) :
arr = critics_arr. copy ( )
for critic in arr:
for film in arr [ critic ] :
if arr [ critic ] [ film ] < 3 :
arr [ critic ] [ film ] = 0
else :
arr [ critic ] [ film ] = 1
return arr
At the output we get the following dictionary:
critics = { 'Lisa Rose' : { 'Superman Returns' : 1 , 'You, Me and Dupree' : 0 , 'The Night Listener' : 1 } ,
'Gene Seymour' : { 'Superman Returns' : 1 , 'The Night Listener' : 1 , 'You, Me and Dupree' : 1 } }
And then we write a function that calculates the coefficient of similarity of the estimates of the two critics.
def tanimoto ( critics_arr, critic1, critic2 ) :
arr = prepare_for_tanimoto ( critics_arr )
a = len ( arr [ critic1 ] )
b = len ( arr [ critic2 ] )
c = 0.0
for film in arr [ critic1 ] :
if arr [ critic1 ] [ film ] == arr [ critic2 ] [ film ] :
c = c + 1
koef = c / ( a + b - c )
return koef
Check the performance of the tanimoto function.
>>> print tanimoto (critics, 'Gene Seymour', 'Lisa Rose')
>>> 0.5
In my opinion, the result is correct. It should be noted that with an increase in the number of assessments for each critic, the accuracy of calculating the similarity coefficient will increase.
If we had a database of estimates, it would be possible to calculate the coefficients of the similarity of interests of people and begin to make recommendations using the Tanimoto method.
Download the sample text here .
Download the full text of all examples from the book on the author's website . You can also find a more complete array with critics.
Source: https://habr.com/ru/post/104901/
All Articles