Once again about sorting
The previous topic, about the assessment of the complexity of the algorithms was very positively evaluated by the habrasoobschestvom. From this I can conclude that the topic of the basic algorithms is very interesting. Today I want to introduce you to the part dedicated to sorting algorithms. It’s not serious to write about basic algorithms for Habr, but it’s still worth telling about Shell sorting, pyramid and fast. (If anyone is interested in reading about the basic methods, you are welcome here )
In 1959, Shell proposed a way to speed up sorting with simple inserts. First, each group of elements separated by k 1 elements from each other is sorted separately. This process is called k 1 sorting. After the first pass, groups of elements are considered, but already separated from each other by k 2 (k 2 <k 1 ) positions, and these groups are also sorted separately. This process is called k 2 sorting. So several iterations are carried out, and at the end the sorting step becomes equal to 1.
A reasonable question arises: will the cost of performing several passes, each of which sorts all the elements, exceed the potential savings? However, each sorting of one group of elements either deals with a relatively small number of them, or the elements are already partially sorted, so relatively few permutations need to be made.
Obviously, the method leads to a sorted array, and it is easy to see that at each step you need to do less work due to previous iterations (since each k i sort combines two groups sorted by the previous k i-1 sort). It is also obvious that any sequence of distances is permissible, so long as the last of them is equal to one. It is not so obvious that the method works better if the decreasing distances are chosen to be different from the power of two.
We give an algorithm for an arbitrary sequence of distances. In total there will be T distances h 1 , h 2 , ..., h T satisfying the conditions: h T = 1, h i + 1 <h i .
Analysis of this algorithm is a complex mathematical problem, which still does not have a complete solution. At the moment it is not known which sequence of distances gives the best result, but it is known that distances should not be multiples of each other. It is necessary that the next passage does not combine the two sequences that were not intersected before. In fact, it is desirable that the sequences intersect as often as possible. This is related to the following theorem: if the sequence after k i is sorted k i + 1 is sorted, then it remains k i sorted.
Knut proposes to use one of the following sequences as successively decreasing (given in reverse): 1,4,13,40,121, ..., where h i-1 = 3 * h i +1 or 1,3,7,15, 31, ..., where h i-1 = 2 * h i +1. In the latter case, a mathematical study shows that when sorting N elements by the Shell algorithm, the costs are proportional to N 1.2 . Although it is much better than N 2 , we will not delve into this method, as there are even faster algorithms.
Simple selection sorting is based on re-selecting the smallest key among the N elements, then among the remaining N-1 elements, etc. Obviously, in order to find the smallest key among the n elements, you need N-1 comparisons, among N-1 elements you need N-2 comparisons, etc. Obviously, the sum of the first N-1 positive integers is (N 2 -N) / 2. This sorting can be improved only if after each viewing more information is saved than just about one smallest element. For example, N / 2 comparisons allow you to define a smaller key in each pair, another N / 4 comparison will give a smaller key in each pair of smaller keys already found, etc. Consider the array 12,18,42,44,55,67,94,6. By making n-1 comparisons, we can build a selection tree, with the smallest key at the root.
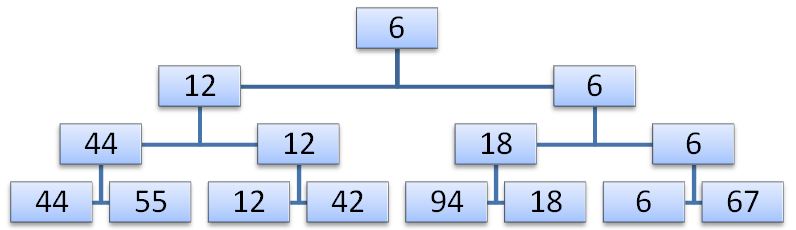
The second step is to descend along the path corresponding to the smallest key and replace it with an empty position in a leaf of the tree, or an element from another branch in intermediate nodes.
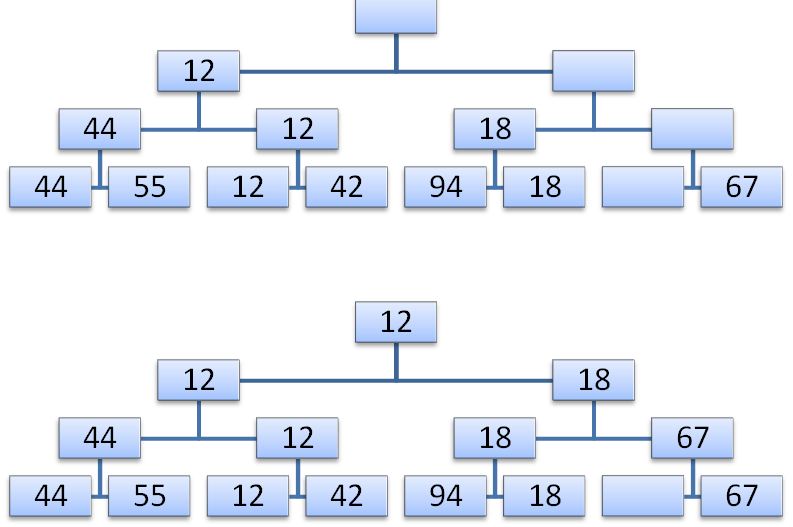
Now the element in the root of the tree will be the next smallest key. Now you can remove it. After N such steps in the tree there will not be a single node with a key, and the sorting process will be completed. Obviously, at each of the N steps, log (N) comparisons are required, so the whole procedure requires about N * log (N) elementary operations (in addition to the N steps that are needed to build the tree). This is a significant improvement not only in comparison with simple methods that require N 2 steps, but also with Shell sorting, which requires N 1.2 steps. Naturally, the complexity of the elementary steps in this algorithm is higher: to save all the information from the previous step, you need to use some tree. Now we need to find a way to efficiently organize this information.
First of all, it is necessary to get rid of the need to store empty values, which, in the end, will fill the entire tree and lead to a large number of unnecessary comparisons. Then we need to find a way to make the tree occupy N units in memory, instead of 2 * N-1, as it happens in the figures. Both goals were achieved in the HeapSort algorithm, so named by its inventor Williams. This algorithm is a radical improvement in conventional tournament sorting.
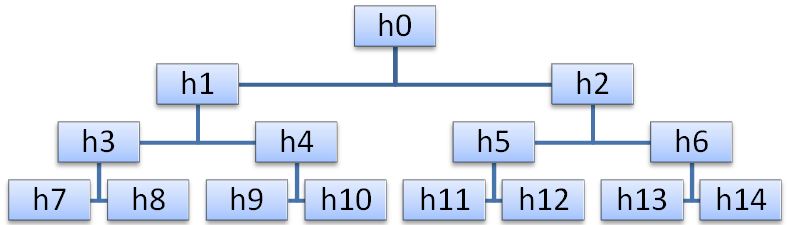
A pyramid (heap) is a sequence of keys h L , h L + 1 , ..., h R (L≥0), such that h i <h 2i + 1 and h i <h 2i + 2 , for i = L ... R / 2-1. It turns out that any binary tree can be represented by an array, as shown in the figure (with the top of the pyramid being its smallest element).
The pyramid expansion algorithm is quite simple. A new pyramid is obtained as follows: first, the added element x is placed on the top of the pyramid, and then sifted down, changing places with the smallest of two descendants, which, accordingly, moves up.
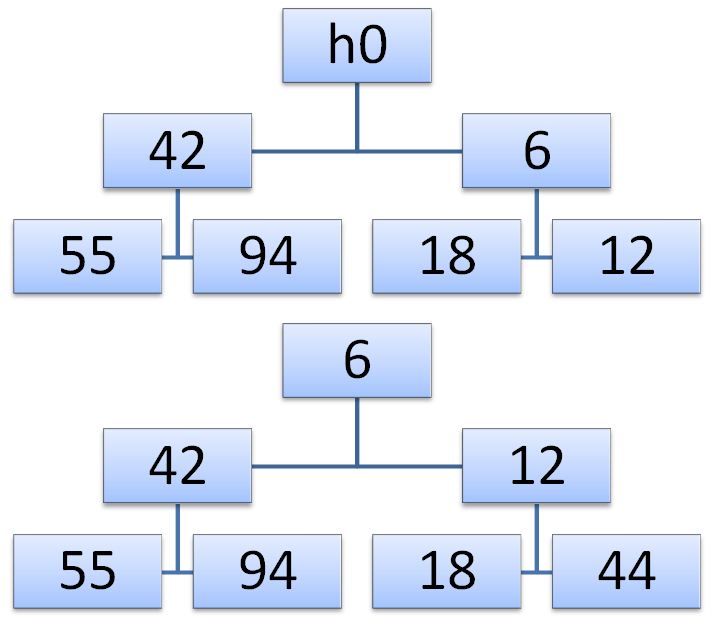
')
In our example, we expand the pyramid with the number h 0 = 44. First, the key 44 changes places with 6, and then with 12. As a result, we obtain the desired tree. We formulate the sifting algorithm in terms of a pair of indices i, j corresponding to the elements that are exchanged at each sieving step.
The method that we will consider was suggested by Floyd. The basis of the method is the sift procedure (screening). If we have an array h 1 ... h N , then its elements with numbers from m = N div 2 to N already form a pyramid (because these elements do not have such pairs i, j, so that j = 2 * i + 1 or j = 2 * i + 2). These elements will form the bottom row of the pyramid. Note that no ordering is required in the bottom row. Then begins the process of expanding the pyramid. And in one step only one element will be included in it, and this element will be put in its place using the sifting procedure, which we will now consider.
The process of obtaining the pyramid can be described as follows:
The pyramid that we get is characterized by the fact that the largest (and not the smallest) key will be stored at its top. In addition, the resulting array will not be fully ordered. In order to achieve complete orderliness, it is necessary to carry out another N siftings and after each of them remove the next element from the top. The question arises, where to store the elements removed from the top. There is a rather beautiful solution to this problem: we need to take the last element of the pyramid (we will call it x), write the element from the top of the pyramid to the position freed from under x, and put the element x in the correct position with the next screening. This process can be described as follows:
Thus, the pyramidal sorting algorithm can be represented by the following code:
In this algorithm, large elements are first sifted to the left, and only then they take final positions on the right side of the sorted array. Because of this, it may seem that the effectiveness of pyramidal sorting is not very high. Indeed, it is better to use other algorithms for sorting a small number of elements, but for large N this sorting is very effective.
In the worst case, the pyramid creation phase requires N / 2 sieving steps, and at each step the elements are sifted through log (N / 2), log (N / 2 + 1), ..., log (N-1) positions. Then the sorting phase requires n-1 screenings with no more than log (N-1), log (N-2), ..., 1 transfers. In addition, you will need n-1 shipments in order to put elements from the top of the pyramid into place. It turns out that even in the worst case pyramidal sorting requires N * log (N) transfers. This property is the most important distinctive feature of this algorithm.
Best performance can be expected if the items initially stand in reverse order. Then the pyramid creation phase does not require shipments. The average number of shipments is N / 2 * log (N), and deviations from this value are quite small.
The two previous methods were based on the principles of insertion and selection. It is time to consider the third, based on the principle of exchange. Bubble sorting turned out to be the worst among all three simple algorithms, but the improvement of exchange sorting gives the best known array sorting method.
The construction of quick sorting is based on the fact that in order to achieve maximum efficiency, it is desirable to perform exchanges between the most distant positions. Suppose we have N elements arranged in the reverse order. You can sort them just for N / 2 exchanges, first exchanging the leftmost and rightmost elements, and then gradually moving inside the array on both sides. Of course, this method will work only if the elements in the array are ordered in the reverse order. Nevertheless, it is on this idea that the method under consideration is built.
Let's try to implement such an algorithm: randomly choose any element (let's call it x). We will scan the array on the left until we find the element a i > x, and then on the right, until we find the element. a j <x Then we will exchange the two found elements and continue this process until both views meet somewhere in the middle of the array. As a result, we obtain an array divided into two parts: the left, with keys smaller (or equal) x, and the right with keys larger (or equal) x. We formulate the separation process as a procedure:
Now, remember that our goal is not just to divide the array, but also to sort it. In fact, there is only one small step from separation to sorting: after dividing the array, you need to apply the same process to both the resulting parts, then to the parts of the parts, etc., until each part consists of one element.
To study the efficiency of quick sorting, you must first examine the behavior of the separation process. After selecting the separating value x, the entire array is scanned, so exactly N comparisons are performed. If we are lucky and the median is always selected as the border (the middle element of the array), then each iteration splits the array in half, and the number of necessary passes is equal to log (N). Then the total number of comparisons is N * log (N), and the total number of exchanges is N * log (N) / 6.
Of course, one cannot expect that with a choice of median it will always be so lucky. Strictly speaking, the probability of this is 1 / N. But it is shown that the expected efficiency of quick sorting is worse than optimal only by a factor of 2 * ln (2).
Even the quick sort algorithm has flaws. With small N, its performance can be assessed as satisfactory, but its advantage lies in the ease of connecting a simple method for processing segments. The worst case problem remains. Suppose that each time the largest value in the shared segment is selected as the dividing element. Then each step will divide a fragment of N elements into two sequences of 1 and N-1 elements, respectively. Obviously, in the worst case, the behavior is estimated to be N 2 . To avoid the worst case, it was proposed to choose the element x as the median of the three values of the segment to be divided. Such an addition does not degrade the algorithm in the general case, but will greatly improve its worst-case behavior.
Efficient sorting methods
Sort inserts with decreasing distance (Shell sort)
In 1959, Shell proposed a way to speed up sorting with simple inserts. First, each group of elements separated by k 1 elements from each other is sorted separately. This process is called k 1 sorting. After the first pass, groups of elements are considered, but already separated from each other by k 2 (k 2 <k 1 ) positions, and these groups are also sorted separately. This process is called k 2 sorting. So several iterations are carried out, and at the end the sorting step becomes equal to 1.
A reasonable question arises: will the cost of performing several passes, each of which sorts all the elements, exceed the potential savings? However, each sorting of one group of elements either deals with a relatively small number of them, or the elements are already partially sorted, so relatively few permutations need to be made.
Obviously, the method leads to a sorted array, and it is easy to see that at each step you need to do less work due to previous iterations (since each k i sort combines two groups sorted by the previous k i-1 sort). It is also obvious that any sequence of distances is permissible, so long as the last of them is equal to one. It is not so obvious that the method works better if the decreasing distances are chosen to be different from the power of two.
We give an algorithm for an arbitrary sequence of distances. In total there will be T distances h 1 , h 2 , ..., h T satisfying the conditions: h T = 1, h i + 1 <h i .
- procedure ShellSort ;
- const
- T = 5 ;
- var
- i , j , k , m : longint ;
- x : longint ;
- h : array [ 1 .. 5 ] of integer ;
- begin
- h [ 1 ] : = 31 ; h [ 2 ] : = 15 ; h [ 3 ] : = 7 ; h [ 2 ] : = 3 ; h [ 1 ] : = 1 ;
- for m : = 1 to T do
- begin
- k : = h [ m ] ;
- for i : = k to N do
- begin
- x : = a [ i ] ;
- j : = i - k ;
- while ( j> = k ) and ( x <a [ j ] ) do
- begin
- a [ j + k ] : = a [ j ] ;
- j : = j - k ;
- end ;
- if ( j> = k ) or ( x> = a [ j ] ) then
- a [ j + k ] : = x
- else
- begin
- a [ j + k ] : = a [ j ] ;
- a [ j ] : = x ;
- end ;
- end ;
- end ;
- end ;
Analysis of this algorithm is a complex mathematical problem, which still does not have a complete solution. At the moment it is not known which sequence of distances gives the best result, but it is known that distances should not be multiples of each other. It is necessary that the next passage does not combine the two sequences that were not intersected before. In fact, it is desirable that the sequences intersect as often as possible. This is related to the following theorem: if the sequence after k i is sorted k i + 1 is sorted, then it remains k i sorted.
Knut proposes to use one of the following sequences as successively decreasing (given in reverse): 1,4,13,40,121, ..., where h i-1 = 3 * h i +1 or 1,3,7,15, 31, ..., where h i-1 = 2 * h i +1. In the latter case, a mathematical study shows that when sorting N elements by the Shell algorithm, the costs are proportional to N 1.2 . Although it is much better than N 2 , we will not delve into this method, as there are even faster algorithms.
Pyramidal sorting (tournament sorting)
Simple selection sorting is based on re-selecting the smallest key among the N elements, then among the remaining N-1 elements, etc. Obviously, in order to find the smallest key among the n elements, you need N-1 comparisons, among N-1 elements you need N-2 comparisons, etc. Obviously, the sum of the first N-1 positive integers is (N 2 -N) / 2. This sorting can be improved only if after each viewing more information is saved than just about one smallest element. For example, N / 2 comparisons allow you to define a smaller key in each pair, another N / 4 comparison will give a smaller key in each pair of smaller keys already found, etc. Consider the array 12,18,42,44,55,67,94,6. By making n-1 comparisons, we can build a selection tree, with the smallest key at the root.

The second step is to descend along the path corresponding to the smallest key and replace it with an empty position in a leaf of the tree, or an element from another branch in intermediate nodes.

Now the element in the root of the tree will be the next smallest key. Now you can remove it. After N such steps in the tree there will not be a single node with a key, and the sorting process will be completed. Obviously, at each of the N steps, log (N) comparisons are required, so the whole procedure requires about N * log (N) elementary operations (in addition to the N steps that are needed to build the tree). This is a significant improvement not only in comparison with simple methods that require N 2 steps, but also with Shell sorting, which requires N 1.2 steps. Naturally, the complexity of the elementary steps in this algorithm is higher: to save all the information from the previous step, you need to use some tree. Now we need to find a way to efficiently organize this information.
First of all, it is necessary to get rid of the need to store empty values, which, in the end, will fill the entire tree and lead to a large number of unnecessary comparisons. Then we need to find a way to make the tree occupy N units in memory, instead of 2 * N-1, as it happens in the figures. Both goals were achieved in the HeapSort algorithm, so named by its inventor Williams. This algorithm is a radical improvement in conventional tournament sorting.
A pyramid (heap) is a sequence of keys h L , h L + 1 , ..., h R (L≥0), such that h i <h 2i + 1 and h i <h 2i + 2 , for i = L ... R / 2-1. It turns out that any binary tree can be represented by an array, as shown in the figure (with the top of the pyramid being its smallest element).

The pyramid expansion algorithm is quite simple. A new pyramid is obtained as follows: first, the added element x is placed on the top of the pyramid, and then sifted down, changing places with the smallest of two descendants, which, accordingly, moves up.

')
In our example, we expand the pyramid with the number h 0 = 44. First, the key 44 changes places with 6, and then with 12. As a result, we obtain the desired tree. We formulate the sifting algorithm in terms of a pair of indices i, j corresponding to the elements that are exchanged at each sieving step.
The method that we will consider was suggested by Floyd. The basis of the method is the sift procedure (screening). If we have an array h 1 ... h N , then its elements with numbers from m = N div 2 to N already form a pyramid (because these elements do not have such pairs i, j, so that j = 2 * i + 1 or j = 2 * i + 2). These elements will form the bottom row of the pyramid. Note that no ordering is required in the bottom row. Then begins the process of expanding the pyramid. And in one step only one element will be included in it, and this element will be put in its place using the sifting procedure, which we will now consider.
- procedure sift ( L , R : integer ) ;
- var
- i , j : integer ;
- x : longint ;
- begin
- i : = L ;
- j : = 2 * i ;
- x : = a [ i ] ;
- if ( j <R ) and ( a [ j ] <a [ j + 1 ] ) then
- j : = j + 1 ;
- while ( j < = R ) and ( x <a [ j ] ) do
- begin
- a [ i ] : = a [ j ] ;
- i : = j ;
- j : = 2 * j ;
- if ( j <R ) and ( a [ j ] <a [ j + 1 ] ) then
- j : = j + 1 ;
- end ;
- a [ i ] : = x ;
- end ;
The process of obtaining the pyramid can be described as follows:
- L : = ( N div 2 ) + 1 ;
- R : = N ;
- while L> 1 do
- begin
- L : = L - 1 ;
- sift ( L , R ) ;
- end ;
The pyramid that we get is characterized by the fact that the largest (and not the smallest) key will be stored at its top. In addition, the resulting array will not be fully ordered. In order to achieve complete orderliness, it is necessary to carry out another N siftings and after each of them remove the next element from the top. The question arises, where to store the elements removed from the top. There is a rather beautiful solution to this problem: we need to take the last element of the pyramid (we will call it x), write the element from the top of the pyramid to the position freed from under x, and put the element x in the correct position with the next screening. This process can be described as follows:
- while R> 1 do
- begin
- x : = a [ 1 ] ;
- a [ 1 ] : = A [ R ] ;
- A [ R ] : = x ;
- R : = R - 1 ;
- sift ( L , R ) ;
- end ;
Thus, the pyramidal sorting algorithm can be represented by the following code:
- procedure HeapSort ;
- procedure sift ( L , R : integer ) ;
- var
- i , j : integer ;
- x : longint ;
- begin
- i : = L ;
- j : = 2 * i ;
- x : = a [ i ] ;
- if ( j <R ) and ( a [ j ] <a [ j + 1 ] ) then
- j : = j + 1 ;
- while ( j < = R ) and ( x <a [ j ] ) do
- begin
- a [ i ] : = a [ j ] ;
- i : = j ;
- j : = 2 * j ;
- if ( j <R ) and ( a [ j ] <a [ j + 1 ] ) then
- j : = j + 1 ;
- end ;
- a [ i ] : = x ;
- end ;
- var
- L , R : integer ;
- x : longint ;
- begin
- L : = ( N div 2 ) + 1 ;
- R : = N ;
- while L> 1 do
- begin
- L : = L - 1 ;
- sift ( L , R ) ;
- end ;
- while R> 1 do
- begin
- x : = a [ 1 ] ;
- a [ 1 ] : = A [ R ] ;
- A [ R ] : = x ;
- R : = R - 1 ;
- sift ( L , R ) ;
- end ;
- end ;
In this algorithm, large elements are first sifted to the left, and only then they take final positions on the right side of the sorted array. Because of this, it may seem that the effectiveness of pyramidal sorting is not very high. Indeed, it is better to use other algorithms for sorting a small number of elements, but for large N this sorting is very effective.
In the worst case, the pyramid creation phase requires N / 2 sieving steps, and at each step the elements are sifted through log (N / 2), log (N / 2 + 1), ..., log (N-1) positions. Then the sorting phase requires n-1 screenings with no more than log (N-1), log (N-2), ..., 1 transfers. In addition, you will need n-1 shipments in order to put elements from the top of the pyramid into place. It turns out that even in the worst case pyramidal sorting requires N * log (N) transfers. This property is the most important distinctive feature of this algorithm.
Best performance can be expected if the items initially stand in reverse order. Then the pyramid creation phase does not require shipments. The average number of shipments is N / 2 * log (N), and deviations from this value are quite small.
Quick sort
The two previous methods were based on the principles of insertion and selection. It is time to consider the third, based on the principle of exchange. Bubble sorting turned out to be the worst among all three simple algorithms, but the improvement of exchange sorting gives the best known array sorting method.
The construction of quick sorting is based on the fact that in order to achieve maximum efficiency, it is desirable to perform exchanges between the most distant positions. Suppose we have N elements arranged in the reverse order. You can sort them just for N / 2 exchanges, first exchanging the leftmost and rightmost elements, and then gradually moving inside the array on both sides. Of course, this method will work only if the elements in the array are ordered in the reverse order. Nevertheless, it is on this idea that the method under consideration is built.
Let's try to implement such an algorithm: randomly choose any element (let's call it x). We will scan the array on the left until we find the element a i > x, and then on the right, until we find the element. a j <x Then we will exchange the two found elements and continue this process until both views meet somewhere in the middle of the array. As a result, we obtain an array divided into two parts: the left, with keys smaller (or equal) x, and the right with keys larger (or equal) x. We formulate the separation process as a procedure:
- procedure partition ;
- var
- i , j : integer ;
- w , x : integer ;
- begin
- i : = 1 ;
- j : = n ;
- // select at random x
- REPEAT
- while a [ i ] <x do
- i : = i + 1 ;
- while x <a [ j ] do
- j : = j - 1 ;
- if i < = j then
- begin
- w : = a [ i ] ;
- a [ i ] : = a [ j ] ;
- a [ j ] : = w ;
- i : = i + 1 ;
- j : = j - 1 ;
- end ;
- UNTIL i> j ;
- end ;
Now, remember that our goal is not just to divide the array, but also to sort it. In fact, there is only one small step from separation to sorting: after dividing the array, you need to apply the same process to both the resulting parts, then to the parts of the parts, etc., until each part consists of one element.
- procedure sort ( L , R : integer ) ;
- var
- i , j : integer ;
- w , x : longint ;
- begin
- i : = L ;
- j : = R ;
- x : = a [ ( L + R ) div 2 ] ;
- REPEAT
- while a [ i ] <x do
- i : = i + 1 ;
- while x <a [ j ] do
- j : = j - 1 ;
- if i < = j then
- begin
- w : = a [ i ] ;
- a [ i ] : = a [ j ] ;
- a [ j ] : = w ;
- i : = i + 1 ;
- j : = j - 1 ;
- end ;
- UNTIL i> j ;
- if L <j then
- sort ( L , j ) ;
- if i <R then
- sort ( i , r ) ;
- end ;
- procedure QuickSort ;
- begin
- sort ( 1 , n ) ;
- end ;
To study the efficiency of quick sorting, you must first examine the behavior of the separation process. After selecting the separating value x, the entire array is scanned, so exactly N comparisons are performed. If we are lucky and the median is always selected as the border (the middle element of the array), then each iteration splits the array in half, and the number of necessary passes is equal to log (N). Then the total number of comparisons is N * log (N), and the total number of exchanges is N * log (N) / 6.
Of course, one cannot expect that with a choice of median it will always be so lucky. Strictly speaking, the probability of this is 1 / N. But it is shown that the expected efficiency of quick sorting is worse than optimal only by a factor of 2 * ln (2).
Even the quick sort algorithm has flaws. With small N, its performance can be assessed as satisfactory, but its advantage lies in the ease of connecting a simple method for processing segments. The worst case problem remains. Suppose that each time the largest value in the shared segment is selected as the dividing element. Then each step will divide a fragment of N elements into two sequences of 1 and N-1 elements, respectively. Obviously, in the worst case, the behavior is estimated to be N 2 . To avoid the worst case, it was proposed to choose the element x as the median of the three values of the segment to be divided. Such an addition does not degrade the algorithm in the general case, but will greatly improve its worst-case behavior.
Source: https://habr.com/ru/post/104697/
All Articles