Natural algorithms. Bee Swarm Behavior Algorithm
The Habrahabr has repeatedly discussed the genetic algorithm, its advantages and disadvantages. But the genetic algorithm (or rather the whole galaxy of its various subspecies) is not the only one of its kind. It belongs to the so-called natural algorithms. They also include the “annealing imitation” algorithm, the “swarm of a bee's behavior” algorithm and the “ant colony behavior” algorithm, and several other almost unknown algorithms.
I would like to dwell on the second, less popular but no less interesting algorithm of synthesis and optimization - the algorithm of the behavior of a swarm of bees - and explain its principle.
To consider the principles of operation of the algorithm of the behavior of a swarm of bees, or the method of the swarm of bees (MCI) let us use the analogy with the real swarm of bees. Imagine a swarm of bees on the field. Their goal is to find a field with the highest density of flowers on the field. Without any idea of ​​the field a priori, the bees begin to search for flowers from random positions with random velocity vectors. Each bee can remember the position where it found the greatest number of flowers and somehow know the areas where other bees found the greatest density of flowers. Choosing between returning to the place where the bee itself discovered the greatest number of flowers, or exploring the place determined by others, like the place with the most flowers, the bee rushes in the direction between two points depending on what has a greater impact on its decision - personal memory. or social reflex. Along the way, the bee can find a place with a higher concentration of flowers than was previously found. In the future, it can be designated as a new place with the greatest concentration of colors, and also as the place of the greatest accumulation of colors, found by the whole swarm. By chance, a bee can fly past a place, with more flowers than any other swarm of bees has found. The whole swarm will then strive towards this place in addition to the observations of each bee. Thus, the bees explore the field: overflying the places with the greatest concentration, they slow down in their direction. Continuously, they check the places that have flown by comparing with those found earlier with the highest concentration of colors, hoping to find the absolute greatest concentration of colors. Ultimately, the bee ends the movement at the site of the field with the greatest concentration of flowers. Soon the whole swarm concentrates around this position. Not being able to find places with a greater concentration of flowers, the bees continuously swarm in the area of ​​the greatest density of flowers. This behavior of bees was the basis of this optimization method.
Particle or Agent - every bee in a swarm is considered as a particle or agent. All particles of the swarm act individually in accordance with one controlling principle: accelerate towards the best personal and best common position, constantly checking the value of the current position.
')
Position - similar to the location of a bee on the field, is represented by coordinates on the xy plane. However, in the general case, you can expand this idea to any N-dimensional space in accordance with the task. This N-dimensional space is the solution domain for an optimized problem, where each set of coordinates represents a solution.
Suitability - by analogy with the example of a bee swarm, the fitness function will be the density of colors: the greater the density, the better the position. The fitness function serves as a means of communication between a physical problem and an optimization algorithm.
Personal best position - by analogy with the bee swarm, each bee remembers the position where she herself discovered the greatest number of flowers. This position with the highest fitness value detected by the bee is known as the personal best position (PNP). Each bee has its own PNP, determined by the way it flew. At each point along the path of movement, the bee compares the value of the suitability of the current position with the value of the PNP. If the current position has a suitability value higher, the PNP value is replaced with the value of the current position.
Global best position - each bee also somehow recognizes the area of ​​greatest concentration of flowers, defined by the whole swarm. This best-fit position is known as the global best position (GNP). For the entire swarm, this is one GNP that each bee aspires to. At every point along the way, each bee compares the suitability of its current position with the HNP. If a bee finds a position with a higher suitability, the HNP is replaced by the current position of the bee.
The first step in the implementation of the MRI is the selection of parameters that need to be optimized, and the determination of the allowable interval for finding the optimal values. Then, in a permissible region, bees are randomly arranged, and vectors and speeds of their movement are also specified. Each particle must then move through the solution space, as if it were a bee in a swarm. The algorithm acts on each particle separately, moving it by a small amount, cycling it through the whole swarm. The following steps are performed for each particle:
Estimation of suitability for a particle, comparison with PNP and GNP. The fitness function, using the coordinates of the particle in the solution space, returns the fitness value for the current position. If this value is greater than the value of the PNP corresponding to this particle, or GNP, then the corresponding positions are replaced with the current position.
Correction of particle velocity. Manipulations with particle velocity are the main element of all optimization. Accurate understanding of the equation used to determine speed is key to understanding the entire optimization process. The particle velocity varies in accordance with the mutual position of the PNP and GNP positions. It tends towards the positions of the greatest suitability according to the following equation
Where:
Is the particle velocity in the nth dimension in the previous step,
Is the coordinate of the particle in the nth dimension
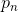- PNP,
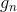- GNP.
The calculation is made for each of N. From this equation it can be seen that the new speed is obtained from the old speed by simple scaling on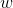
, and adding the direction of GNP and PNP for that particular direction. 
and 
- These are scale factors that determine the relative mutual "attraction" to the PNP and GNP. They are sometimes regarded as cognitive and social factors. - this is the coefficient that determines how the particle has its memory on the PNP, and - coefficient determining the impact on the particle of the rest of the swarm. Increase involves the study of the space of solutions by moving each particle in the direction of its PNP; an increase suggests a study of the estimated global maximum. The rand () random number function returns a number between -1 and 1. In the general case, the two occurrences of the rand () function are two different function calls. Most implementations use two independent random variables to stochasticly change the relative gravity of HNP and PNP. This introduction of the random element in the optimization is intended to simulate a minor unpredictable component of the real behavior of the swarm. 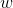referred to as “inertial weight” and this number (selected between 0 and 1) reflects the extent to which the particle remains true to its original course, unaffected by HNP and PNP.
We set the boundaries initially, but nowhere in the formulas and methods they were not mentioned. So how do you take them into account? There are several answers to this question.
For example, walls can be made absorbing. When a particle hits the boundary of the solution space in one of the dimensions, the velocity in this dimension is zeroed, and the particle will eventually be returned to the specified solution space. This means that the boundaries - “walls” absorb the energy of particles trying to allow the allowed region. Or reflect the speed of the particle when it flies to the "wall". But the most effective solution turned out to be “invisible walls”. A particle can safely fly out beyond their limits, but being outside the allowed area, the values, the values ​​obtained by it are simply not taken into account, until it returns back.
As a result, I want to note that the swarm of the bees method can be effectively distributed into several parallel processes, due to which its speed will increase significantly.
Compared to a genetic algorithm, the operators of which can be implemented in different ways, there is only one operator - speed calculation, which makes it easier to use.
In the swarm method, bees can easily determine the achievement of a global minimum point, while in genetic algorithms this is significantly complicated.
The concept of these methods is based on two completely different natural processes: the MCI is based on the social behavior of the swarm, and the genetic algorithm mimics the process of evolution and natural selection. Due to this, it is possible to combine these two methods.
I would like to dwell on the second, less popular but no less interesting algorithm of synthesis and optimization - the algorithm of the behavior of a swarm of bees - and explain its principle.
To consider the principles of operation of the algorithm of the behavior of a swarm of bees, or the method of the swarm of bees (MCI) let us use the analogy with the real swarm of bees. Imagine a swarm of bees on the field. Their goal is to find a field with the highest density of flowers on the field. Without any idea of ​​the field a priori, the bees begin to search for flowers from random positions with random velocity vectors. Each bee can remember the position where it found the greatest number of flowers and somehow know the areas where other bees found the greatest density of flowers. Choosing between returning to the place where the bee itself discovered the greatest number of flowers, or exploring the place determined by others, like the place with the most flowers, the bee rushes in the direction between two points depending on what has a greater impact on its decision - personal memory. or social reflex. Along the way, the bee can find a place with a higher concentration of flowers than was previously found. In the future, it can be designated as a new place with the greatest concentration of colors, and also as the place of the greatest accumulation of colors, found by the whole swarm. By chance, a bee can fly past a place, with more flowers than any other swarm of bees has found. The whole swarm will then strive towards this place in addition to the observations of each bee. Thus, the bees explore the field: overflying the places with the greatest concentration, they slow down in their direction. Continuously, they check the places that have flown by comparing with those found earlier with the highest concentration of colors, hoping to find the absolute greatest concentration of colors. Ultimately, the bee ends the movement at the site of the field with the greatest concentration of flowers. Soon the whole swarm concentrates around this position. Not being able to find places with a greater concentration of flowers, the bees continuously swarm in the area of ​​the greatest density of flowers. This behavior of bees was the basis of this optimization method.
Method language
Particle or Agent - every bee in a swarm is considered as a particle or agent. All particles of the swarm act individually in accordance with one controlling principle: accelerate towards the best personal and best common position, constantly checking the value of the current position.
')
Position - similar to the location of a bee on the field, is represented by coordinates on the xy plane. However, in the general case, you can expand this idea to any N-dimensional space in accordance with the task. This N-dimensional space is the solution domain for an optimized problem, where each set of coordinates represents a solution.
Suitability - by analogy with the example of a bee swarm, the fitness function will be the density of colors: the greater the density, the better the position. The fitness function serves as a means of communication between a physical problem and an optimization algorithm.
Personal best position - by analogy with the bee swarm, each bee remembers the position where she herself discovered the greatest number of flowers. This position with the highest fitness value detected by the bee is known as the personal best position (PNP). Each bee has its own PNP, determined by the way it flew. At each point along the path of movement, the bee compares the value of the suitability of the current position with the value of the PNP. If the current position has a suitability value higher, the PNP value is replaced with the value of the current position.
Global best position - each bee also somehow recognizes the area of ​​greatest concentration of flowers, defined by the whole swarm. This best-fit position is known as the global best position (GNP). For the entire swarm, this is one GNP that each bee aspires to. At every point along the way, each bee compares the suitability of its current position with the HNP. If a bee finds a position with a higher suitability, the HNP is replaced by the current position of the bee.
Algorithm
The first step in the implementation of the MRI is the selection of parameters that need to be optimized, and the determination of the allowable interval for finding the optimal values. Then, in a permissible region, bees are randomly arranged, and vectors and speeds of their movement are also specified. Each particle must then move through the solution space, as if it were a bee in a swarm. The algorithm acts on each particle separately, moving it by a small amount, cycling it through the whole swarm. The following steps are performed for each particle:
Estimation of suitability for a particle, comparison with PNP and GNP. The fitness function, using the coordinates of the particle in the solution space, returns the fitness value for the current position. If this value is greater than the value of the PNP corresponding to this particle, or GNP, then the corresponding positions are replaced with the current position.
Correction of particle velocity. Manipulations with particle velocity are the main element of all optimization. Accurate understanding of the equation used to determine speed is key to understanding the entire optimization process. The particle velocity varies in accordance with the mutual position of the PNP and GNP positions. It tends towards the positions of the greatest suitability according to the following equation
Where:
Is the particle velocity in the nth dimension in the previous step, Is the coordinate of the particle in the nth dimension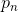 - PNP, 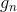- GNP.The calculation is made for each of N. From this equation it can be seen that the new speed is obtained from the old speed by simple scaling on
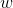, and adding the direction of GNP and PNP for that particular direction. and - These are scale factors that determine the relative mutual "attraction" to the PNP and GNP. They are sometimes regarded as cognitive and social factors. - this is the coefficient that determines how the particle has its memory on the PNP, and - coefficient determining the impact on the particle of the rest of the swarm. Increase involves the study of the space of solutions by moving each particle in the direction of its PNP; an increase suggests a study of the estimated global maximum. The rand () random number function returns a number between -1 and 1. In the general case, the two occurrences of the rand () function are two different function calls. Most implementations use two independent random variables to stochasticly change the relative gravity of HNP and PNP. This introduction of the random element in the optimization is intended to simulate a minor unpredictable component of the real behavior of the swarm. 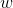referred to as “inertial weight” and this number (selected between 0 and 1) reflects the extent to which the particle remains true to its original course, unaffected by HNP and PNP.Border conditions
We set the boundaries initially, but nowhere in the formulas and methods they were not mentioned. So how do you take them into account? There are several answers to this question.
For example, walls can be made absorbing. When a particle hits the boundary of the solution space in one of the dimensions, the velocity in this dimension is zeroed, and the particle will eventually be returned to the specified solution space. This means that the boundaries - “walls” absorb the energy of particles trying to allow the allowed region. Or reflect the speed of the particle when it flies to the "wall". But the most effective solution turned out to be “invisible walls”. A particle can safely fly out beyond their limits, but being outside the allowed area, the values, the values ​​obtained by it are simply not taken into account, until it returns back.
Conclusion
As a result, I want to note that the swarm of the bees method can be effectively distributed into several parallel processes, due to which its speed will increase significantly.
Compared to a genetic algorithm, the operators of which can be implemented in different ways, there is only one operator - speed calculation, which makes it easier to use.
In the swarm method, bees can easily determine the achievement of a global minimum point, while in genetic algorithms this is significantly complicated.
The concept of these methods is based on two completely different natural processes: the MCI is based on the social behavior of the swarm, and the genetic algorithm mimics the process of evolution and natural selection. Due to this, it is possible to combine these two methods.
Source: https://habr.com/ru/post/104055/
All Articles