Rubik's Cube in 20 steps
Any position of the Rubik's Cube can be solved in no more than 20 steps.
A few years ago it was proved that there is a solution for the Rubik's Cube in 23 moves. Now this number has been reduced to 20. It took 35 (thirty-five) years of computer time donated by Google to do this.
Each solution block used its own algorithm - a sequence of steps to achieve the desired configuration. For example, one algorithm was designed to solve the upper face, and the other - to position the middle edges. There are many different algorithms that differ in the degree of complexity and the number of steps required, but those that a person can remember usually require more than 40 steps.
')
It is reasonable to believe that God can use a more efficient algorithm that solves the problem in the shortest number of steps. This algorithm is known as the “God algorithm”. The number of steps in the worst case is called the number of God. In the end, it was shown that this number is 20.
After the invention of the Rubik's Cube, it took fifteen years to find a position that is probably solved in 20 steps. 15 years after this, we will prove that 20 steps are enough for any position.
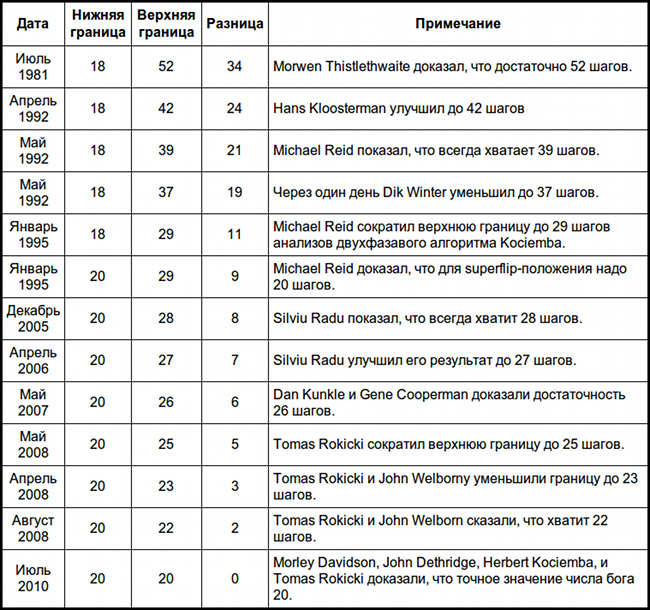
By 1980, the lower limit was set at 18, and the upper limit, probably around 80. The table below summarizes all the results:
How did we deal with the 43 252 003 274 489 856 000 positions of the Rubik's Cube?
We have broken the big task into 2 217 093 120 smaller subtasks: each consisted of 19,508,428,800 different positions. One such subtask fits easily into the memory of a modern computer, and this method made it possible to quickly obtain a solution.
If you turn the Rubik's Cube left-right or up-down, then, in fact, nothing will change: the number of steps in the solution will remain the same. Instead of solving all these positions, you can get a solution for one and extend it to rotated positions. There are 24 different orientations in space and 2 mirror positions of the Cube for each position, which allows reducing the number of solved positions by 48 times. If we use similar reasoning and use the search for the problem of “covering a set”, then the number of subtasks decreases from 2 217 093 120 to 55 882 296.
The optimal solution contains a sufficient number of steps, but no more than necessary. Since one position is already known, which requires 20 steps, we can not look for the optimal solution for each position, but only solutions in 20 or less steps. This speeds up the task many times over.
We had the opportunity to solve 55 882 296 subtasks on Google’s facilities and perform all the calculations in a few weeks. Google did not disclose the characteristics of computers, but it took 1.1 billion seconds of computer time (Intel Nehalem, four-core, 2.8GHz) to perform the calculations.
We have known for 15 years that there are positions that require 20 steps, but we have proved that for one position and not more.
Positions with solutions in 20 steps are rare, but it is quite possible to meet them in reality. The probability of meeting such a position varies from 10 ^ (- 9) to 10 ^ (- 8). We do not know the exact number of such positions. The table gives an estimate of the number of positions for each solution length.
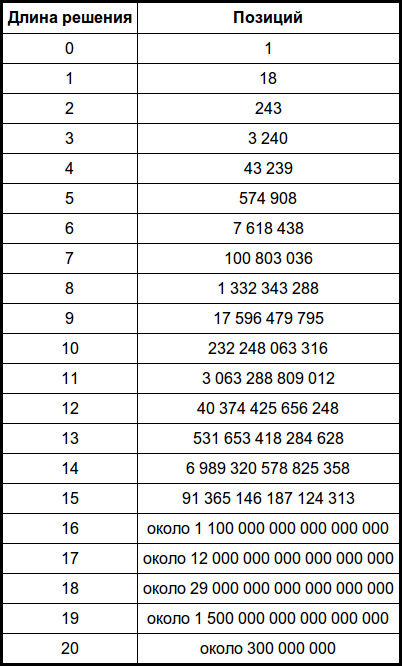
For lengths of 16 or more, numbers are approximate. Our studies confirmed all the initial data up to and including line 14, and line 15 is a new result. On August 11, we found 12 million positions with a solution length of 20. This position was the most difficult for our programs:

A few years ago it was proved that there is a solution for the Rubik's Cube in 23 moves. Now this number has been reduced to 20. It took 35 (thirty-five) years of computer time donated by Google to do this.
Each solution block used its own algorithm - a sequence of steps to achieve the desired configuration. For example, one algorithm was designed to solve the upper face, and the other - to position the middle edges. There are many different algorithms that differ in the degree of complexity and the number of steps required, but those that a person can remember usually require more than 40 steps.
')
It is reasonable to believe that God can use a more efficient algorithm that solves the problem in the shortest number of steps. This algorithm is known as the “God algorithm”. The number of steps in the worst case is called the number of God. In the end, it was shown that this number is 20.
After the invention of the Rubik's Cube, it took fifteen years to find a position that is probably solved in 20 steps. 15 years after this, we will prove that 20 steps are enough for any position.
History of the number of God
By 1980, the lower limit was set at 18, and the upper limit, probably around 80. The table below summarizes all the results:

How we did it
How did we deal with the 43 252 003 274 489 856 000 positions of the Rubik's Cube?
- We divided all positions into 2 217 093 120 sets - 19 508 428 800 positions in each.
- We reduced the number of sets for the solution to 55,888,296 based on symmetry and covering the set.
- We did not look for an optimal solution, but only solutions with a length of 20 steps or less.
- We wrote a program that finds a solution for one set in 20 seconds.
- It took 35 years of computer time to search for solutions of all configurations in each of 55,888,296 sets.
Division of the space of positions
We have broken the big task into 2 217 093 120 smaller subtasks: each consisted of 19,508,428,800 different positions. One such subtask fits easily into the memory of a modern computer, and this method made it possible to quickly obtain a solution.
Symmetry
If you turn the Rubik's Cube left-right or up-down, then, in fact, nothing will change: the number of steps in the solution will remain the same. Instead of solving all these positions, you can get a solution for one and extend it to rotated positions. There are 24 different orientations in space and 2 mirror positions of the Cube for each position, which allows reducing the number of solved positions by 48 times. If we use similar reasoning and use the search for the problem of “covering a set”, then the number of subtasks decreases from 2 217 093 120 to 55 882 296.
Good and optimal solutions
The optimal solution contains a sufficient number of steps, but no more than necessary. Since one position is already known, which requires 20 steps, we can not look for the optimal solution for each position, but only solutions in 20 or less steps. This speeds up the task many times over.
Equipment
We had the opportunity to solve 55 882 296 subtasks on Google’s facilities and perform all the calculations in a few weeks. Google did not disclose the characteristics of computers, but it took 1.1 billion seconds of computer time (Intel Nehalem, four-core, 2.8GHz) to perform the calculations.
The most difficult pose
We have known for 15 years that there are positions that require 20 steps, but we have proved that for one position and not more.
Positions with solutions in 20 steps are rare, but it is quite possible to meet them in reality. The probability of meeting such a position varies from 10 ^ (- 9) to 10 ^ (- 8). We do not know the exact number of such positions. The table gives an estimate of the number of positions for each solution length.

For lengths of 16 or more, numbers are approximate. Our studies confirmed all the initial data up to and including line 14, and line 15 is a new result. On August 11, we found 12 million positions with a solution length of 20. This position was the most difficult for our programs:

Source: https://habr.com/ru/post/103843/
All Articles