Cartesian tree: Part 2. Valuable information in the tree and multiple operations with it

Table of Contents (for now)

Part 1. Description, operation, application.
Part 2. Valuable information in the tree and multiple operations with it.
Part 3. The Cartesian tree by implicit key.
To be continued ...

Theme of today's lecture

Last time we met - let's say frankly, very extensively acquainted with - the concept of a Cartesian tree and its basic functionality. Only up to now we have used it in one and only way: as a “quasi-balanced” search tree. That is, let us be given an array of keys, add randomly generated priorities to them, and get a tree in which each key can be searched for, added, and deleted in logarithmic time and a minimum of effort. It sounds good, but not enough.

Fortunately (or unfortunately?), Real life is not limited to such trifling tasks. What is today and will be discussed. The first question on the agenda is the so-called K-th ordinal statistics, or an index in the tree, which will smoothly lead us to store user information at the vertices, and finally - to the countless manipulations with this information that may be required. Go.
')

Looking for an index

In mathematics, the K-th order statistic is a random variable that corresponds to the K-th largest element of a random sample from a probability space. Too clever. Let's return to the tree: at each moment of time we have a Cartesian tree, which could have changed significantly since its initial construction. We are required to very quickly find the Kth key in this tree in ascending order — in fact, if we represent our tree as a constantly maintained sorted array, then it is just access to the element under the K index. At first glance, it is not very clear how to organize it: we have keys in the N tree, and they are scattered across the structure at random.


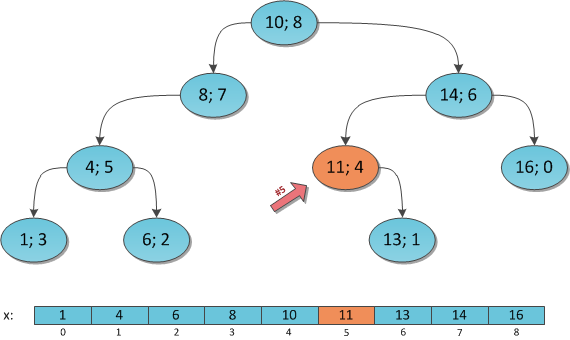
Although, frankly, not as horrible. We know the property of the search tree — for each vertex, its key is more than all the keys of its left subtree, and less than all the keys of the right subtree. Therefore, to arrange the keys of a tree in a sorted order, it is enough to conduct a so-called In-Order walk around it, that is, to walk through the whole tree, following the principle “first recursively bypass the left subtree, then the key of the root itself, and then the recursively right subtree”. If every key we encounter in this way is written to a list, then in the end we will get a completely sorted list of all the nodes of the tree. Whoever does not believe, can carry out the above procedure on the deramid from the picture just above - will receive an array from the same picture.

The above reasoning allows us to write for the Cartesian tree an iterator in order to use the standard language tools ( foreach , etc.) to walk through its elements in ascending order. In C #, to do this, you can simply write an in-order bypass function and use the yield return , and in those where there is no such powerful functionality, you will have to go one of two ways. Or store at each vertex a link to the “next” element in the tree, which gives an additional expense of valuable memory. Or, to write a non-recursive tree traversing through your own stack, which is somewhat more complicated, but it will improve both the speed of the program and the cost of memory.

Of course, this approach should not be regarded as a complete solution of the problem, because it requires O (N) time, and this is unacceptable. But you can try to improve it if we knew immediately which parts of the tree we should not go in, because there are guaranteed larger or smaller elements in order. And this is quite realistic to realize, if we remember for each vertex of the tree, how many elements we will have to go around during a recursive entry into it. That is, we will store at each vertex its subtree size .

The figure shows the same tree with the sizes of subtrees affixed at each vertex.

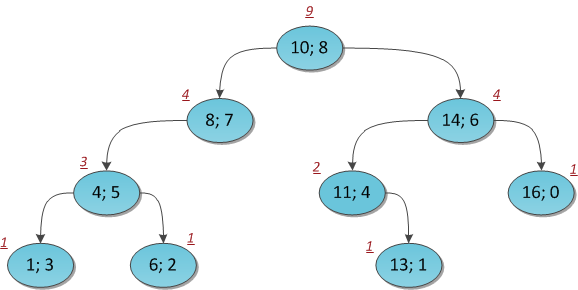
Then suppose that we honestly calculated the number of vertices in each subtree. We now find the Kth element in the indexing starting from zero (!).

The algorithm is clear: we look at the root of the tree and the size of its left subtree S _L , the size of the right one is not even needed.
If S _L = K, then we have found the required element, and this is the root.
If S _L > K, then the desired element is somewhere in the left subtree, descend there and repeat the process.
If S _L <K, then the desired element is somewhere in the right subtree. Reduce K by the number S _L +1 in order to correctly respond to the sizes of the subtrees on the right, and repeat the process for the right subtree.

I will model this search for K = 6 on the same tree:
Vertex (10; 8), S _L = 4, K = 6. Go to the right, decreasing K by 4 + 1 = 5.
Vertex (14; 6), S _L = 2, K = 1. Go left, without changing K.
Vertex (11; 4), S _L = 0 (no left son), K = 1. Go right, decreasing K by 0 + 1 = 1.
Vertex (13; 1), S _L = 0 (no left son), K = 0. The key is found.
Answer: the key under the index 6 in the Cartesian tree is equal to 13.

In principle, this entire passage resembles a simple key search in a binary search tree - it’s still just going down the tree comparing the parameter you are looking for with the parameter in the current vertex, and depending on the situation we turn left or right. I will say in advance - we will meet more than once with a similar situation in different algorithms, it is quite typical for various binary trees. The traversal algorithm is so typical that it is easy to template. As you can see, recursion is not even needed here, we can do with a simple cycle with a couple of variables that change with each iteration.

In a functional language, you can write a solution through recursion, and it will look and be read much more beautifully, without losing a bit of performance: a tail recursion, and the compiler immediately optimizes it in the same ordinary cycle. For those who know functional programming, but doubt in my words - Haskell code:
data Ord a => Treap a = Null
| Node { key :: a , priority :: Int , size :: Int , left :: (Treap a) , right :: (Treap a) }

sizeOf :: ( Ord a) => Treap a -> Int
sizeOf Null = 0
sizeOf Node {size = s} = s

kthElement :: ( Ord a) => (Treap a) -> Int -> Maybe a
kthElement Null _ = Nothing
kthElement (Node key _ _ left right) k
| sizeLeft == k = Just key
| sizeLeft < k = kthElement left k
| sizeLeft > k = kthElement right (k - sizeLeft - 1)
where sizeLeft = sizeOf left


Speaking of performance. The search time for the Kth element is obviously O (log ₂ N), we just went down from the top to the depth of the tree.

In order not to offend readers, in addition to the functional, I will also give the traditional source code in C #. In it, in the standard workpiece of the Treap class, given in the first part, one more integer field Size is added - the size of the subtree, as well as the useful SizeOf function for its reception.

 public static int SizeOf(Treap treap) { return treap == null ? 0 : treap.Size; } public int? KthElement(int K) { Treap cur = this; while (cur != null) { int sizeLeft = SizeOf(cur.Left); if (sizeLeft == K) return cur.x; cur = sizeLeft > K ? cur.Left : cur.Right; if (sizeLeft < K) K -= sizeLeft + 1; } return null; } 

The key issue is still the fact that we still do not know how to maintain the correct size values ​​in the tree. After all, after the first addition to the tree of a new key, all these numbers will go to ashes, and recalculate them each time again - O (N)! But no. O (N) it would take after some operation that completely re-arranged the tree into an incomprehensible structure. And here is the addition of a key that acts more carefully and does not touch the whole tree, but only its small part. So you can do with less blood.

As you remember, with us everything is done, so to speak, through Split and Merge. If we adapt these two main functions to support additional information in the tree - in this case, the sizes of the subtrees - then all other operations will automatically be performed correctly, because they do not make any changes to the tree (except for creating elementary trees from one vertex where Size needed Do not forget to set the default to 1!).
I will start by modifying the operation Merge.

Recall the procedure for performing Merge. She first chose the root for a new tree, and then recursively merged one of its subtrees with another tree and wrote down the result in place of the harvested subtree. I will deal with the case when it was necessary to merge the right subtree, the second is symmetrical. Like last time, recursion will help us a lot.

Let's make the induction hypothesis: let after the execution of the Merge on subtrees, everything is already calculated correctly in them. Then we have the following state of affairs: in the left subtree the dimensions are calculated correctly, since nobody touched him; right is also calculated correctly, because This is the result of Merge. Restore justice remains only at the root of the new tree! Well, just recalculate it before completion ( size = left.size + right.size + 1 ) , and now Merge has completely created an entire new tree, at each vertex of which is the correct size of the subtree.

The source code of the Merge will change slightly: to the recalculation line before returning the answer. It is marked with a comment.

 public void Recalc() { Size = SizeOf(Left) + SizeOf(Right) + 1; } public static Treap Merge(Treap L, Treap R) { if (L == null) return R; if (R == null) return L; Treap answer; if (Ly > Ry) { var newR = Merge(L.Right, R); answer = new Treap(Lx, Ly, L.Left, newR); } else { var newL = Merge(L, R.Left); answer = new Treap(Rx, Ry, newL, R.Right); } answer.Recalc(); // ! return answer; } 

Exactly the same situation awaits us with the operation Split, which is also based on a recursive call. Let me remind you: here, depending on the key value in the root of the tree, we recursively divided according to the specified key either the left or right subtree of the original, and one of the results was hung back, and the second was returned separately. Again, let for the sake of uniqueness, we recursively divide T.Right.

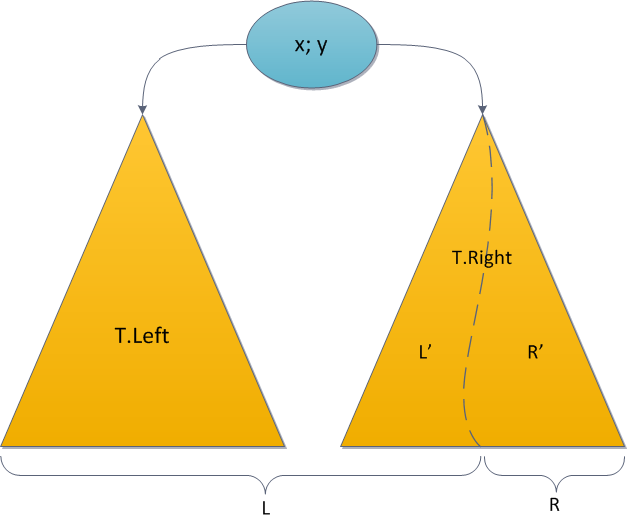
The familiar induction hypothesis - let the recursive calls Split calculate everything correctly - it will help us this time too. Then the dimensions in T.Left are correct - nobody touched them; dimensions in L 'are correct - this is the left result Split; dimensions in R 'are correct - this is the right result of the split. Before completion, justice must be restored at the root (x; y) of the future L tree - and the answer is ready.

The source code of the new Split, in which the two added lines recalculate the Size value in the root L or R, depending on the variant.

 public void Recalc() { Size = SizeOf(Left) + SizeOf(Right) + 1; } public void Split(int x, out Treap L, out Treap R) { Treap newTree = null; if (this.x <= x) { if (Right == null) R = null; else Right.Split(x, out newTree, out R); L = new Treap(this.x, y, Left, newTree); L.Recalc(); //   L! } else { if (Left == null) L = null; else Left.Split(x, out L, out newTree); R = new Treap(this.x, y, newTree, Right); R.Recalc(); //   R! } } 

The “restoration of justice” under discussion - recalculation of the value at the top — I singled out into a separate function. This is the base line, which holds the functionality of the entire Cartesian tree. And when in the second half of the article we will have multiple multiple operations, each with its own “recovery”, it will be much more convenient to change it in one single place than throughout the entire class code. Such a function has one common property: it assumes that everything is valid in the left son, everything is valid in the right son, and on the basis of these data recalculates the parameter in the root. Thus, it is possible to support any additional parameters that are calculated from the descendants, the sizes of the subtrees are just a particular example.

Welcome to the real world

Let's go back to the real life. In it, the data that you have to store in the tree is not limited to the key alone. And with this data constantly have to make some kind of manipulation. For example, in this article I will call such a new field Duchi Cost .

So, let us at the entrance constantly receive (and sometimes delete) the keys x , and each of them is associated with the corresponding price - Cost . And you need to support in all this porridge quick requests for maximum prices. You can ask the maximum in the whole structure, but you can only on some subsegment of it: for example, the user may be interested in the maximum price for 2007 (if the keys are related to time, this can be interpreted as a maximum price request on a set of such elements, where A ≤ x < b ).

This is not a problem, because the maximum is also an excellent candidate for the function of “justice restoration”. Enough to write like this:

 public double Cost; //  public double MaxTreeCost; public static double CostOf(Treap treap) { return treap == null ? double.NegativeInfinity : treap.MaxTreeCost; } public void Recalc() { MaxTreeCost = Math.Max(Cost, Math.Max(CostOf(Left), CostOf(Right))); } 

The same situation with the minimum, and with the sum, and with some Boolean characteristics of the element (the so-called "coloring" or "marked"). For example:

 //  public double SumTreeCost; public static double CostOf(Treap treap) { return treap == null ? 0 : treap.SumTreeCost; } public void Recalc() { SumTreeCost = Cost + CostOf(Left) + CostOf(Right); } 

Or:

 public bool Marked; //  public bool TreeHasMarked; public static bool MarkedOf(Treap treap) { return treap == null ? false : treap.TreeHasMarked; } public void Recalc() { TreeHasMarked = Marked || MarkedOf(Left) || MarkedOf(Right); } 

The only thing to remember in such cases is to initialize these parameters in the constructor when creating new individual vertices.

As they would say in the functional world, we are performing to some extent the convolution of a tree.

Thus, we are able to query the value of the parameter for the entire tree - it is stored in the root. Inquiries on podotrezkakh also not difficult, if again recall the property of the binary search tree. The key of each vertex is greater than all the keys of the left subtree and less than all the keys of the right subtree. Therefore, we can virtually assume that there is an associated key interval associated with each vertex, which, in theory, can be found in it and in its subtree. So, at the root it is an interval (-∞; + ∞) , at its left son (-∞; x) , right - (x; + ∞) , where x is the key value in the root. All intervals open on both sides, X among the keys of the right subtree can not meet. If we allow the same keys in the tree and, as in the first part, force the comparator to throw them all into the same subtree — say, to the left, then the interval for the left son will be (-∞; x] .

For clarity, I will show in the figure the corresponding interval for each vertex of the Cartesian tree already investigated.

It is now clear that the parameter stored at the vertex is responsible for the value of the corresponding characteristic (maximum, sum, etc.) for all keys on the interval of this vertex.

And we can respond to requests at intervals [A; B) (in C ++ and similar languages ​​it is generally more convenient to operate with half-open intervals that include the left end and do not include the right end; in the future I will do so).
Someone familiar with the segment tree may think that it is worthwhile to use the same recursive descent, gradually localizing the current vertex to one that fully corresponds to the desired interval or a piece of it. But we will do it easier and faster, reducing the task to the previous one.

Masterfully possessing scissors, we divide the tree first, using the key A-1. The right-hand result Split, which stores all keys greater than or equal to A, is divided again - this time by key B. In the middle we will get a tree with all the elements for which the keys belong to the desired interval. To find out the parameter, it’s enough to look at its value in the root - after all, Split has already done all the hard work of restoring justice for each tree for us :)

The query time is obviously O (log ₂ N): two executions of Split. Source code for maximum:

 public double MaxCostOn(int A, int B) { Treap l, m, r; this.Split(A - 1, out l, out r); r.Split(B, out m, out r); return CostOf(m); } 

The power of deferred computing

Today's aerobatics is the ability to change user information in the course of a tree’s life. It is clear that after changing the value of Cost at some vertex, all of our previous parameters, which have accumulated answers for the values ​​in their subtrees, are no longer valid. You can, of course, walk around the whole tree and recount them again, but this is O (N) again, and will not go into any gate. What to do?

If we are talking about a simple change in Cost in a single vertex, then this is not such a problem. At first, moving from top to bottom, we find the necessary element. We change the information in it. And then, moving back upwards to the root, we simply recalculate the values ​​of the parameters by the standard function - after all, this change will not affect any other subtrees, except for those that we visited on the way from root to top. The source code, I believe, does not make much sense; the task is trivial: solve it with at least recursion, at least in two cycles, the runtime is still O (log ₂ N).

Life becomes much more fun if you need to support multiple operations . Let us have a Cartesian tree, in each of its peaks stored user information Cost . And we want to add the same number A to each value of Cost in the tree (or subtree - see the reasoning about the intervals). This is an example of a multiple operation, in this case adding a constant on the segment. And here you will not get by with a simple passage to the root.

Let's get in each vertex an additional parameter, let's call it Add . Its essence is as follows: it will signal that the entire subtree growing from a given vertex is supposed to add a constant to Add . It turns out to be such a late addition: if you need to change the values ​​to A, in some subtree we change only the root Add in this subtree, as if giving a promise to descendants that “sometime in the future you all will be additionally added, but we’ll will not be until it is required. "

Then the Cost request from the root of the tree should perform one more additional action, adding the root Add to Cost , and regard the received sum as the actual Cost , as if lying in the root of the tree. The same with requests for additional parameters, for example, the sum of prices in the tree: we have the correct (!) SumTreeCost value in the root, which stores the sum of all the elements of the tree, but not taking into account that we must add to all these elements Add . To obtain a truly correct value of the sum with all pending operations, it suffices to add the SumTreeCost value to SumTreeCost multiplied by Size — the number of elements in the subtree.

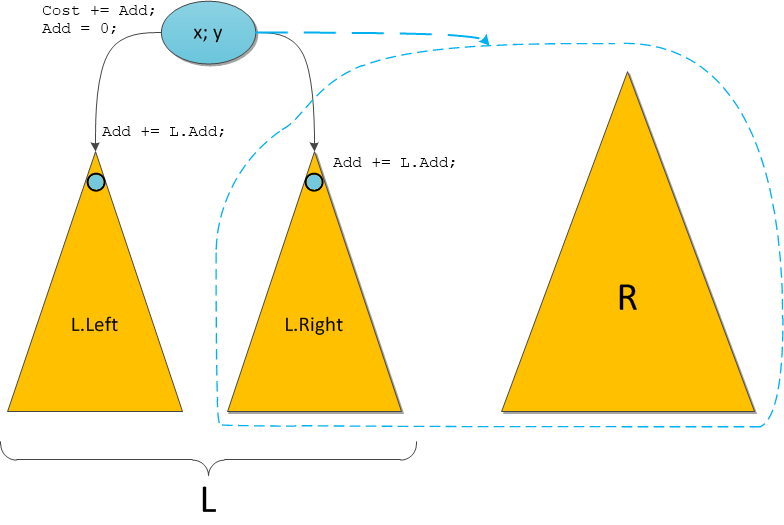
So far, it is not very clear what to do with the standard operations of the Cartesian tree - Split and Merge - and when we need to still fulfill the promise and add to the descendants the promised them Add . Now consider these issues.

Take up the Split operation again. Since the original tree is divided into two new ones, and we lose the original one, the pending addition will have to be partially completed. Namely: let the recursive call Split divides our right subtree T.Right. Then we will carry out such manipulations:

• Fulfill the promise in the root, add to the root Cost value of the root Add .

  T.Cost + = T.Add; 

• “Let’s pull down” the promise to the left: Add also required for the entire left subtree. But since the recursion to the left does not go, we don’t need to actively touch this subtree. Just write the promise.

  T.Left.Add + = T.Add; 

• “Let's make a promise” to the right: the Add right is also required for the entire right subtree. This must be done before the recursive call so that the Split operation manipulates the correct Cartesian tree. The recursion will do the next update itself.

  T.Right.Add + = T.Add; 

• Make a recursive call. Split returned us two valid Cartesian trees.
• Since we honestly fulfilled the promise in the root, and honestly recorded promises for our descendants in memory, the root Add should be reset.

  T.Add = 0; 

• Further subtree attachments in Split are performed as usual. As a result - two correct Cartesian trees with actual information on promises: somewhere fulfilled, somewhere only deferred, but actual.

All operations are indicated on the new Split chart.

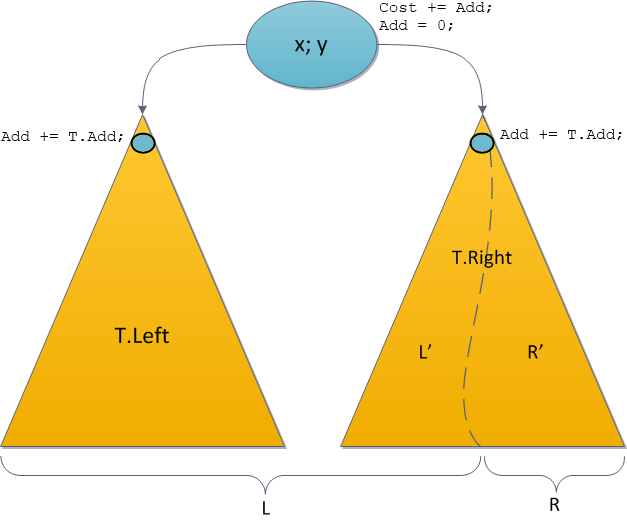
Note that the actual updates are carried out only in those vertices that the Split operation will follow recursively, for the rest, we will at best lower the promise a bit lower. The same situation will be with Merge.

The new Merge basically does the same. Let him need to recursively merge the right L.Tight subtree with the right input tree R. Then do the following:

• Fulfill the promise in the root L.

  L.Cost + = L.Add; 

• “Let's unleash” the promise to the descendants of L - for the future.

  L.Left.Add + = L.Add;
   L.Right.Add + = L.Add; 

• The promise is completely fulfilled - you can forget about it.

  L.Add = 0; 

• Making the necessary recursive call Merge (L.Right, R) , because now both its arguments are valid Cartesian trees. And she will return us the correct tree too.
• Suspend the returned tree with the right son, as before. In the end - again Cartesian tree with relevant information on the promises.



Now, when we are able to make inquiries in the root and change on the whole tree, it is not difficult to scale this solution for sub-splices, simply applying the same principle as several paragraphs above.
We make two Split calls, selecting the subtree corresponding to the required key interval in a separate tree.
Let us increase the root promise of this tree Addfor a given A. We obtain a valid tree with a pending addition.
Let us merge again all three trees together with two calls Mergeand write in the place of the original one. Now, keys at a given interval honestly live with the promise that all of them sometime in the future are supposed to add A.
The source code of this manipulation can be left as an exercise for the reader :)

Do not forget to restore justice in the roots after all operations by calling a new version of the function Recalc. This new version should take into account deferred additions, as already described in the story of requests.

Finally, I note that multiple operations, of course, are not limited to only one addition on the segment. You can also “paint” on the segment — set the Boolean parameter to all elements, change it — set all values Coston the segment to one value, and so on, which only the imagination of the programmer comes up with. The main condition for the operation is that it can be pushed down from the root to the descendants by O (1) , transferring the delayed promise just below the tree, as we did with Merge and Split. And, of course, information should be easily restored from the promise at the time of the request, otherwise there is no point in making a garden.

Summary

We have learned to support various user additional information in a Cartesian tree, and to carry out with it a huge number of multiple manipulations, with each request or change, whether at a single vertex or in a segment, is performed in logarithmic time. Coupled with the elementary properties of the Cartesian tree, described in the first part, this already represents a huge scope for its practical use in any system where it is necessary to store significant amounts of data, and periodically request any statistics from these data.

But in the next part I will make a Cartesian tree a small modification that will turn it into a tool of truly enormous power for everyday needs. This miracle will be called a "Cartesian tree with an implicit key."

Thank you all for your attention.