Cartesian wood: Part 1. Description, operations, applications

Table of Contents (for now)

Part 1. Description, operation, application.

Part 2. Valuable information in the tree and multiple operations with it.

Part 3. The Cartesian tree by implicit key.

To be continued ...



The Cartesian tree (cartesian tree, treap) is a beautiful and easily implemented data structure that allows you to perform many high-speed operations on arrays of your data with minimal effort. That is characteristic, on Habrakhabr I found its only mention in the review post of the highly respected winger , but then the continuation of that cycle never followed. It's a shame by the way.



I will try to cover everything that I know about the topic - despite the fact that I know relatively not so much, there will be enough material for two, or even three. All algorithms are illustrated with source codes in C # (and since I am a lover of functional programming, somewhere in the epilogue, it will come to F # as well - but it is not necessary to read this :). So let's get started.

')

Introduction

As an introduction, I recommend reading the post about binary search trees of the same winger , because without understanding what a tree is, the search tree, as well as without knowing the estimates of the complexity of the algorithm, much of the material in this article will remain for you in Chinese writing. It's a shame, right?



The next item on our mandatory program is a heap . I think many well-known data structures, but I still give a brief overview.

Imagine a binary tree with some data (keys) in the vertices. And for each vertex we necessarily demand the following: her key is strictly greater than the keys of her immediate sons. Here is a small example of a valid heap:

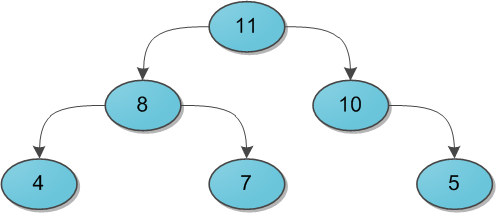
I will immediately say to a note that it is absolutely not necessary to think about the heap solely as a structure whose parent has more than its descendants. Nobody forbids to take the opposite option and assume that the parent is smaller than the descendants - the main thing is to choose one for the whole tree. For the needs of this article it will be much more convenient to use the option with the “more” sign.

Now the question remains how to add and remove items from it in a heap. Firstly, these algorithms require a separate place for inspection, and secondly, we still will not need them.

Problems

When it comes to search trees (you have already read the recommended article, right?), The main question that is posed to the structure is the speed of operations, regardless of the data stored in it, and the sequence of their receipt. Thus, a binary search tree guarantees that a search for a specific key in this tree will be done in O (H), where H is the height of the tree. But what could be the height - the devil knows. Under unfavorable circumstances, the height of a tree can easily become N (the number of elements in it), and then the search tree degenerates into a regular list - and why is it then needed? To achieve this situation, it is enough to add elements from 1 to N in the ascending queue to the search tree - with the standard addition algorithm to the tree, we get the following picture:



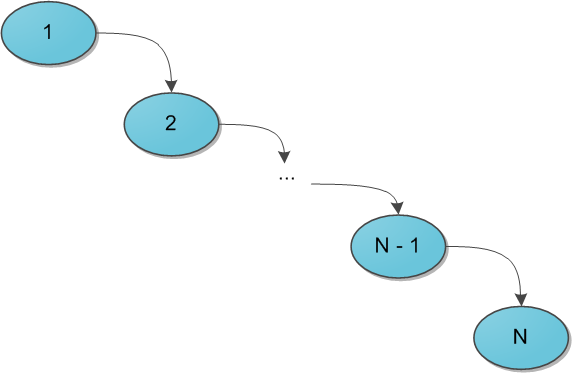
A huge number of so-called balanced search trees were invented - roughly speaking, in which, as the tree exists, each operation on it maintains the optimality of the maximum depth of the tree. The optimal depth is of the order O (log ₂ N) - then the same order has the execution time of each search in the tree. The data structures supporting such depth are many, the most famous here is a red-ebony or AVL-tree. Their distinctive feature in the majority is a difficult implementation, based on the size of the damn pile of cases in which you can get confused. Its simplicity and beauty favorably differ, on the contrary, the Cartesian tree, and even gives us that logarithmic time in some way, but only with rather high probability ... however, about such details and subtleties later.

Definition

So, we have the tree data — the x keys (hereinafter, the key is assumed to be the same information that we store in the tree; when later we need to separate user information from the keys, I’ll say a little). Let's add to them another parameter in the pair - y , and call it a priority . Now we will build such a magic tree, which stores at each vertex two parameters, and at the same time the keys are the search tree, and the priorities are the heap . Such a tree will be called Cartesian.

By the way: in English literature the name treap is very popular, which clearly shows the essence of the structure: tree + heap. In the Russian-speaking language, it is sometimes possible to find those composed according to the same principle: deramid (tree + pyramid) or ducha (tree + heap).

Why is a tree called Cartesian? This will immediately become clear as soon as we try to draw it. Take a set of key-priority pairs and place the corresponding points (x, y) on the coordinate grid. And then we connect the corresponding vertices with lines, forming a tree. Thus, the Cartesian tree fits perfectly on the plane due to its limitations, and its two main parameters, the key and the priority, are, in a sense, coordinates. The result of the construction is shown in the figure: on the left in the standard tree notation, on the right - on the Cartesian plane.





So far it is not very clear why this is necessary. And the solution is simple, and it lies in the following statements. First, let a set of keys be given: there are many different ones that can be constructed from the correct search trees, including the list-like ones. But after adding priorities to them, a tree from these keys can be built only one single thing, regardless of the order in which the keys arrive. This is pretty obvious.

And secondly, let's now make our priorities random. That is, we simply associate with each key a random number from a sufficiently large range, and it will serve as the corresponding player. Then the resulting Cartesian tree with a very high, tending to 100% probability will have a height not exceeding 4 log ₂ N. (I will leave this fact here without proof.) So, although it may not be perfectly balanced, the search time for the key is such a tree will still be of the order of O (log ₂ N), which we, in fact, achieved.

Another interesting approach is not to make priorities random, but to recall that we have a huge amount of some additional user information, which, as a rule, we have to store in the treetops. If there is reason to believe that this information is inherently quite random (the user's birthday, for example), then you can try to use it for personal gain. Take as a priority either directly information, or the result of some function from it (only then the function must be reversible in order to restore information from priorities, if necessary). However, it is necessary to act here at your own peril and risk - if after a while the tree becomes strongly unbalanced and the whole program begins to be significantly slowed down, you will have to immediately tinker with something to save the situation.

Further, for simplicity, we assume that all keys and all priorities in trees are different. In fact, the possibility of key equality does not create any particular problems; you just need to clearly define where elements equal to a given x will be located - either only in its left subtree, or only in the right one. Equality of priorities in theory is also not a particular problem, except for contamination of evidence and reasoning with special cases, but in practice it is better to avoid it. Random generation of integer priorities is quite suitable in most cases, real between 0 and 1 - in almost all cases.

Before starting the story about operations, I’ll give you a class C # preset that will implement our Cartesian tree.

public class Treap { public int x; public int y; public Treap Left; public Treap Right; private Treap(int x, int y, Treap left = null, Treap right = null) { this.x = x; this.y = y; this.Left = left; this.Right = right; } //   ... } 

For simplicity, I made x and y of int type, but it is clear that in their place there could be any type, the instances of which we can compare with each other - that is, anyone implementing IComparable or IComparable<T> in terms of C #. In Haskell, it could be any type from the Ord class, in F # any with restrictions on the comparison operator, in Java it implements the Comparable<T1> interface, and so on.

Magic glue and scissors

On the agenda of pressing issues - how to work with Cartesian wood. The question of how to build it from a raw set of keys in general, I will postpone a bit, but for now let's assume that some kind soul has already built the initial tree for us, and now we need to change it if necessary.



All the ins and outs of the Cartesian wood work consists of two main operations: Merge and Split . With the help of them all other popular operations are elementarily expressed, so let's start with the basics.



Operation Merge takes as input two Cartesian trees L and R. It is required from it to merge them into one, also correct, Cartesian tree T. It should be noted that operation Merge can work not with any pairs of trees, but only with those for which all keys of one tree (L) do not exceed the keys of the second (R). (Pay special attention to this condition - it will be useful to us again and again in the future!)





The Merge algorithm is very simple. Which element will become the root of the future tree? Obviously, with the highest priority. We have two candidates for maximum priority - only the roots of two source trees. Let's compare their priorities; let for unambiguity the priority y of the left root is greater, and the key in it is equal to x. The new root is defined, now it is worth thinking what elements will appear in its right subtree, and which - in the left one.



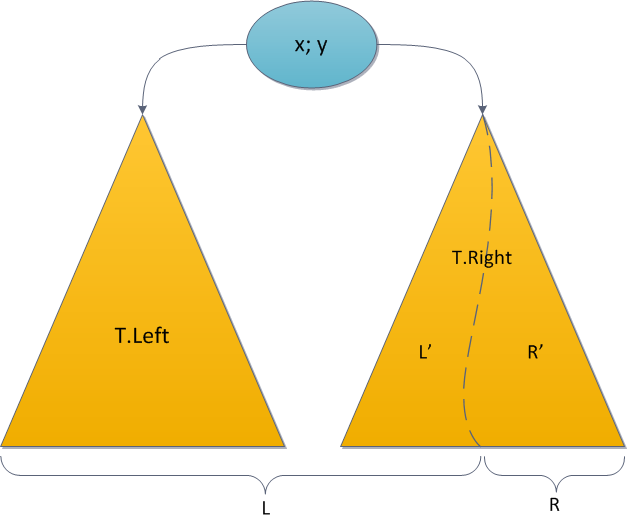
It is easy to understand that the whole tree R will be in the right subtree of the new root, because the keys have more than x by condition. Similarly, the left subtree of the old root L.Left has all the keys smaller than x, and the left subtree should remain, and the right L.Tight subtree should be right for the same reasons, but it’s not clear where to put its elements and where are the elements of the tree R?



Wait, why is it unclear? We have two trees, the keys in one are fewer keys in the other, and we need to somehow combine them and attach the result to the new root as the right subtree. Simply recursively call Merge for L.Right and tree R, and use the tree returned by it as a new right subtree. The result is obvious.



The figure in blue shows the right subtree of the result tree after the Merge operation and the connection from the new root to this subtree.



The symmetric case - when the priority in the root of the tree R is higher - is dealt with similarly. And, of course, we must not forget about the basis of recursion, which in our case occurs if one of the trees L and R, or both at once, are empty.



Merge source code:

 public static Treap Merge(Treap L, Treap R) { if (L == null) return R; if (R == null) return L; if (Ly > Ry) { var newR = Merge(L.Right, R); return new Treap(Lx, Ly, L.Left, newR); } else { var newL = Merge(L, R.Left); return new Treap(Rx, Ry, newL, R.Right); } } 

Now about the operation Split. The input is a valid Cartesian tree T and a key x ₀ . The task of the operation is to divide the tree into two so that in one of them (L) all elements of the source tree with keys smaller than x _{0 are found} , and in the other (R) - with large ones. There are no special restrictions on the tree.





We argue in a similar way. Where is the root of the tree T? If its key is less than x ₀ , then in L, otherwise in R. Again, suppose for the sake of unambiguity that the key of the root was less than x ₀ .



Then you can immediately say that all elements of the left subtree of T will also appear in L - their keys, too, will all be less than x ₀ . Moreover, the root T will also be the root L, since its priority is greatest in the whole tree. The left subtree of the root will remain completely unchanged, but the right one will decrease - you will have to remove elements with keys greater than x ₀ from it and take it to the R tree. Save the rest of the keys as a new right subtree L. See the identical task again, recursion again suggests!



Take the right subtree and recursively split it by the same key x ₀ into two trees L 'and R'. Then it becomes clear that L 'will become the new right subtree of the tree L, and R' is just the tree R - it consists of those and only those elements that are larger than x ₀ .



The symmetric case in which the root key is greater than x ₀ is also completely identical. The basis of recursion here is when some of the subtrees are empty. Well, the source code of the function:

 public void Split(int x, out Treap L, out Treap R) { Treap newTree = null; if (this.x <= x) { if (Right == null) R = null; else Right.Split(x, out newTree, out R); L = new Treap(this.x, y, Left, newTree); } else { if (Left == null) L = null; else Left.Split(x, out L, out newTree); R = new Treap(this.x, y, newTree, Right); } } 

By the way, pay attention: the trees, which are output by the Split operation, are suitable as input data for the Merge operation: all the keys of the left tree do not exceed the keys on the right. This valuable circumstance will come in handy in just a few paragraphs.



The last question is the time of the Merge and Split. From the description of the algorithm, it can be seen that for each iteration of the recursion Merge reduces the total height of two trees to be merged by at least one, so that the total operation time does not exceed 2H, that is, O (H). And with Split, everything is quite simple - we work with a single tree, its height decreases with each iteration, too, by at least one, and the asymptotic behavior of the operation is also O (H). And since the Cartesian tree with random priorities, as already mentioned, has a high probability close to the logarithmic height, the Merge and Split work for the desired O (log ₂ N), and this gives us tremendous scope for their use.

Tree operations

Now, when you and I are perfectly fluent in glue and scissors, it is absolutely no work just with the help of them to implement the most necessary actions with the Cartesian tree: adding an element to the tree and removing it. I will give the simplest version of their implementation, based entirely on Merge and Split. It will work for all the same logarithmic time, however, as ACM Olympians say, will differ by a greater constant: that is, the order of time dependency on the size of the tree will still be O (log ₂ N), but the exact work time will differ several times - in constant times. Say, 4 log ₂ N versus just log ₂ N. In practice, this difference is hardly felt until the size of the tree reaches truly galactic sizes.

There are also optimal implementations of both add-ons with deletions and other necessary deramid operations, the constant of which is much smaller. I will definitely bring these implementations in one of the following parts of the cycle, and also talk about the pitfalls associated with the use of a faster option. Pitfalls are primarily associated with the need to support additional requests to the tree and store special information in it ... however, I won’t be bothering the reader with this, the time will come to multiple operations with the tree (an extremely important feature!).

So, let us be given a Cartesian tree and some element x that needs to be inserted into it (as we remember, in the context of the article it is assumed that all elements are different and there is no X in the tree yet). I would like to apply the approach from the binary search tree: go down the keys, each time choosing a path left or right, until we find a place where we can insert our x, and add it. But this decision is wrong, because we have forgotten about priorities. The place where the search tree algorithm wants to add a new vertex uniquely satisfies the constraints of the search tree with respect to x, but may violate the heap constraint with y. So you have to act a little higher and more abstract.



The second solution is to present the new key as a tree from a single vertex (with a random priority y), and merge it with the original one with the help of Merge. This is again wrong: in the source tree there may be vertices with keys greater than x, and then we break the promise given to the Merge function regarding the relationship between its input trees.



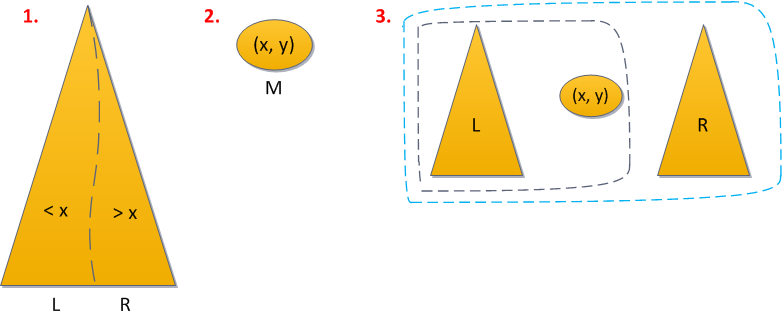
The problem can be fixed. Remembering the versatility of the Split / Merge operations, the solution is suggested almost immediately:

1. Divide (split) tree by key x into tree L, with keys less than X, and tree R, with large ones.
2. Create a tree M from a single key from a single vertex (x, y), where y is a random priority just generated.
3. Combine (merge) in turn L with M, then what happened - with R.

All steps of the algorithm can be illustrated.



We have 1 Split application here, and 2 Merge applications - total O (log ₂ N) operation time. Short source code is attached.

 public Treap Add(int x) { Treap l, r; Split(x, out l, out r); Treap m = new Treap(x, rand.Next()); return Merge(Merge(l, m), r); } 

There are no issues with deletion either. Let us ask you to remove the element with the key x from the Cartesian tree. Now I assume that you have dealt with the equality of keys, giving preference to the left side: in the right subtree of the vertex with the key x, other elements are not found with the same key, but in the left can. Then perform the following sequence of actions:

1. Divide the tree first by key x-1. All elements that are smaller or equal to x-1, went to the left result, then the desired element - in the right.
2. We divide the right result by the key x (here it is worth being careful with equality!). All elements with keys greater than x went to the new right result, and all smaller or equal to x went to the “middle” (left from the right). But since the strictly smaller ones after the first step were all sifted out, the middle tree is the desired element.
3. Now simply combine the left tree with the right one, without the middle one, and the deramid is left without the x keys.

Now I understand why I constantly focused on how it is necessary to take into account the equality of keys. Say, if your comparator thought that elements with equal keys should be sent to the right subtree, then in the first step you would have to divide by the key x, and in the second - by x + 1. But if there were no specifics on this issue at all, then the deletion procedure in this variant could not even accomplish what was desired - after the second step, the middle tree would remain empty, and the desired element would slip away somewhere, either to the left or to the right, and look for him now.



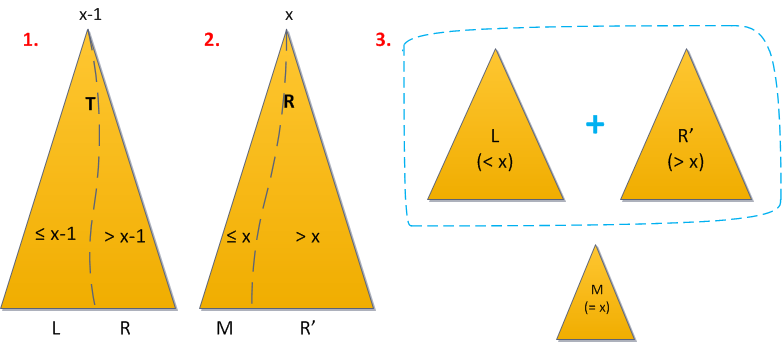
The operation time is still O (log ₂ N), since we applied Split 2 times and Merge 1 times.

Source:

 public Treap Remove(int x) { Treap l, m, r; Split(x - 1, out l, out r); r.Split(x, out m, out r); return Merge(l, r); } 

Act of creation

Now, knowing the algorithm for adding an element to a finished Cartesian tree, we can provide the simplest way to build a tree from an incoming set of keys: simply add them in turn by the standard algorithm, starting from a tree from one vertex - the first key. Bearing in mind that the add operation is performed in logarithmic time, we get the total execution time of a full tree construction - O (N log ₂ N).



Interesting, but you can quickly?



As it turned out, in some cases - yes. Let's imagine that the keys to us come in ascending order. This, in principle, may well happen if these are some kind of newly created identifiers with auto increment. So, in this case, there is a simple algorithm for constructing a tree in O (N). True, we will have to pay for this temporary overhead from memory: to store a reference to its ancestor for each vertex of the tree under construction (in fact, it is not even necessary for each, but these are subtleties).



We will keep a link to the last added vertex in the tree. In terms of compatibility, it will be right in it - after all, it has the key of the largest of all keys of the tree built at the moment. Now suppose that the next key x arrives at the input with some priority y . Where to put it?



The last vertex is the rightmost, therefore it has no right son. If its priority is greater than the y being added, then you can simply assign a new vertex to the right-hand son and move to the next key at the entrance with a clear conscience. Otherwise, you have to think. The new top still has the largest key, so ultimately it will definitely become the rightmost top of the tree. Therefore, it does not make sense to look for a place to insert it anywhere, except along the rightmost branch. We only need to find a place where the priority of the vertex is greater than y. So, we will rise from the rightmost up the branch, each time checking the priority of the current top of the inspected. In the end, we will either come to the root, or stop somewhere in the middle of the branch.



Suppose we come to the root. Then it turns out that y is greater than all the priorities in the tree. We have no choice but to make (x, y) a new root and attach an old tree to it with our left son.



If we did not reach the root, the situation is similar. At some vertex of the right branch (x ₀ , y ₀ ) we have y ₀ > y . And its immediate right descendant has a priority less than y. To keep the search tree structure by keys, and make (x, y) the most right in the tree, we hang it as a new right son to (x ₀ , y ₀ ) , and the entire old right subtree becomes the left subtree (x, y).



To make it clearer, I will illustrate with examples. Take a Cartesian tree and show what happens if you try to add certain vertices to it. The key is the same everywhere (22), and the priority is vary.

y = 4:



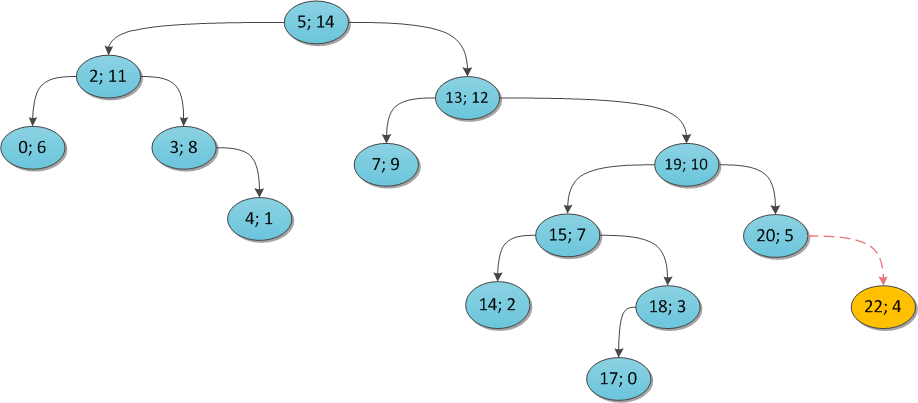
y = 16:



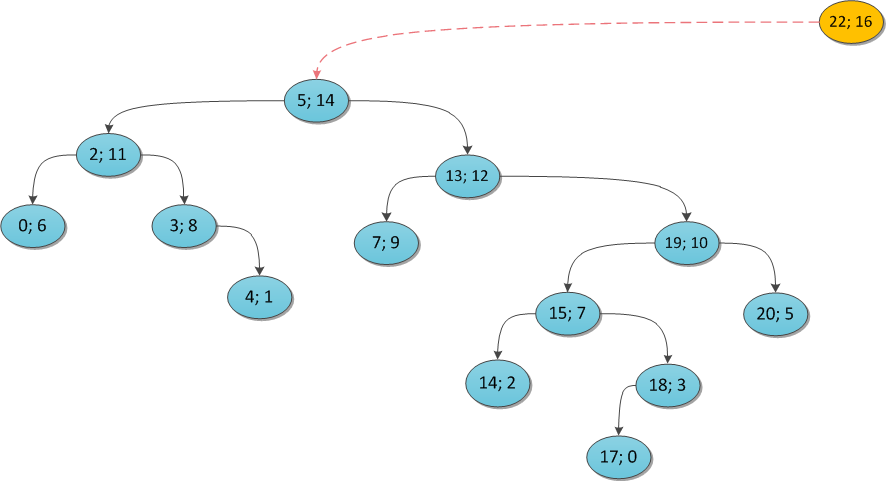
y = 11:





Why does this algorithm work for O (N)? Note that you will visit each tree peak a maximum of two times:

• when it is directly added;
• perhaps by adding some other one, as long as it stays in the right branch. Immediately after that, it will leave the right branch and will not be visited more.

Thus, the total number of transitions does not exceed 2N, and the asymptotic construction is O (N).



For a snack - the source code for building a given array of keys and priorities. Here it is assumed that each vertex of the tree has the Parent property, and also that an optional parameter with the same name is already used in the private vertex constructor (the fifth in a row).

 public static Treap Build(int[] xs, int[] ys) { Debug.Assert(xs.Length == ys.Length); var tree = new Treap(xs[0], ys[0]); var last = tree; for (int i = 1; i < xs.Length; ++i) { if (last.y > ys[i]) { last.Right = new Treap(xs[i], ys[i], parent: last); last = last.Right; } else { Treap cur = last; while (cur.Parent != null && cur.y <= ys[i]) cur = cur.Parent; if (cur.y <= ys[i]) last = new Treap(xs[i], ys[i], cur); else { last = new Treap(xs[i], ys[i], cur.Right, null, cur); cur.Right = last; } } } while (last.Parent != null) last = last.Parent; return last; } 

Summary

We have built a tree data structure with the following properties:

• has almost guaranteed logarithmic height relative to the number of its vertices;
• allows for logarithmic time to search for any key in the tree, add it and delete it;
• the source code of all its methods does not exceed 20 lines, they are easily understood and it is extremely difficult to make mistakes in them
• contains some overhead memory, compared with the truly self-balancing trees, to store priorities.

In principle, the result is quite powerful. However, some may still be unclear whether it was worth for him to fence such a large garden with such a bunch of text. Worth it. The point is that the possibilities of the Cartesian tree and the potential for its use are far from being limited to the functions described in this article. This is only a preface.



In the following parts:

1. Multiple operations on a Cartesian tree (looking for O (log ₂ N) sum, maximum, etc.)
2. Cartesian tree by implicit key (or how to improve a regular array)
3. Accelerated implementations of Cartesian functions (and their problems)
4. The functional implementation of the Cartesian tree on F #.

Sources

Sources indicate once and for all, they are the same for all planned articles.



First of all, when writing these articles, I base myself on Vital Goldstein's lecture told at the ACM ICPC Kharkiv Winter School on Programming in 2010. It can be downloaded from the school’s video gallery (year 2010, day 2) as soon as it starts working again, because in the last few days the server has messed up something disastrous.



Maxim's site “e-maxx” Ivanova is a rich storehouse of information on various algorithms and data structures used in sports programming. In particular, there is on it and an article about the Cartesian tree .



In the famous book Kormen, Leiserson, Rivest, Stein “Algorithms: Construction and Analysis” you can find evidence that the expectation of the height of a random binary search tree is O (log ₂ N), although its definition of a random search tree is different from what we used here.



For the first time, deramids were proposed in an article by Seidel, Raimund; Aragon, Cecilia R. (1996), "Randomized Search Trees" . In principle, there you can find the full amount of information on the topic.



That's all for now. I hope you were interested :)