Topological sorting
Topological sort is one of the main algorithms on graphs, which is used to solve many more complex problems.
The task of topological sorting of a graph is as follows: specify a linear order on its vertices, so that any edge leads from a vertex with a smaller number to a vertex with a higher number. Obviously, if there are cycles in the graph, then there is no such order.
An oriented network (or simply a network) is called an infinite-oriented graph. In tasks of this kind, only finite networks are considered.
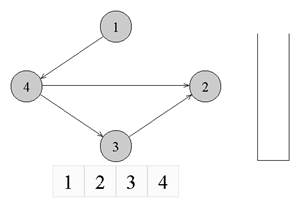
It can be seen from the figure that the graph is not sorted, since the edge from vertex number 4 leads to the vertex with lower number ( 2 ).
There are several ways of topological sorting - from the most famous:
Depth-first search or depth-by-depth search (English Depth-first search , abbreviated DFS ) is one of the ways to bypass the graph. The search algorithm is described as follows: for each vertex not traversed, it is necessary to find all not traversed adjacent vertices and repeat the search for them.
More information about the search in depth can be found in the article on Habré .
We start the detour in depth, and when the vertex is processed, we put it on the stack. At the end of the detour to the depths, the vertices are pulled from the stack. New numbers are assigned in order of pulling out of the stack.
Color: 3 colors are used during the depth crawl. Initially, all vertices are white. When the top is found, paint it gray. When the list of all vertices adjacent to it is viewed, we paint it black.
I think it will be easier to consider this algorithm by example:

↑ We have an infinite oriented graph. Initially, all the vertices are white, and the stack is empty. Begin the detour from the top of number 1.
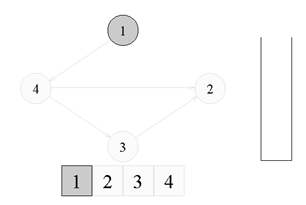
Go to the top of number 1. Paint it gray.
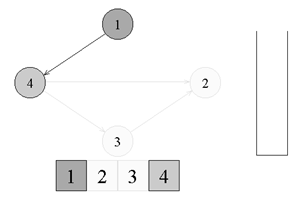
↑ There is an edge from vertex number 1 to vertex number 4. Go to vertex number 4 and paint it gray.
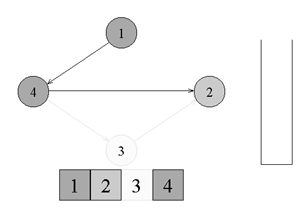
↑ There is an edge from vertex number 4 to vertex number 2. Go to vertex number 2 and paint it gray.

↑ From vertex number 2, there are no edges going to black vertices. We return to vertex number 4. We color vertex number 2 in black and put it on the stack.
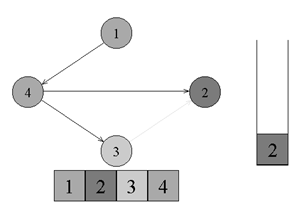
There is an edge from vertex number 4 to vertex number 3. Go to vertex number 3 and paint it gray.
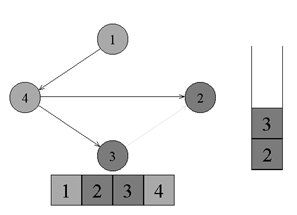
↑ From vertex number 3 there are no edges going to black vertices. We return to vertex number 4. We color vertex number 3 in black and put it on the stack.
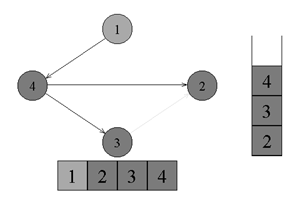
↑ From vertex number 4 there are no edges going to black vertices. We return to vertex number 1. Paint the vertex number 4 in black and put it on the stack.
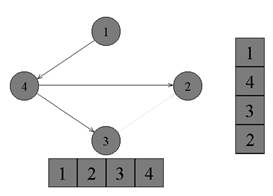
↑ From vertex number 1, there are no edges going to black vertices. Paint it black and put it on the stack. Point crawl over.
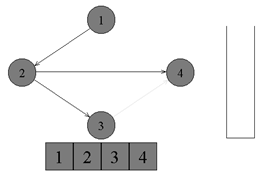
↑ In turn, we get all the vertices from the stack and assign them the numbers 1, 2, 3, 4, respectively. Topology sorting algorithm completed. Graph sorted.
')
Topological sorting is used in a variety of situations, for example, when parallelizing algorithms, when according to some description of the algorithm it is necessary to compile a dependency graph of its operations and, sorting it topologically, determine which of the operations are independent and can be performed in parallel (simultaneously). An example of the use of topological sorting is the creation of a site map, where a tree-like system of sections takes place. (if interested - to google)
As for the implementation - here you can find 22 lines of code implementing this algorithm (everything is carefully commented out)
The task of topological sorting of a graph is as follows: specify a linear order on its vertices, so that any edge leads from a vertex with a smaller number to a vertex with a higher number. Obviously, if there are cycles in the graph, then there is no such order.
An oriented network (or simply a network) is called an infinite-oriented graph. In tasks of this kind, only finite networks are considered.

↑ An example of a directed unsorted graph to which topological sorting is applicable
It can be seen from the figure that the graph is not sorted, since the edge from vertex number 4 leads to the vertex with lower number ( 2 ).
There are several ways of topological sorting - from the most famous:
- Demucron Algorithm
- Sorting method for representing the graph in the form of several levels
- Topological sorting method using depth traversal
The essence of the algorithm
Depth-first search or depth-by-depth search (English Depth-first search , abbreviated DFS ) is one of the ways to bypass the graph. The search algorithm is described as follows: for each vertex not traversed, it is necessary to find all not traversed adjacent vertices and repeat the search for them.
More information about the search in depth can be found in the article on Habré .
We start the detour in depth, and when the vertex is processed, we put it on the stack. At the end of the detour to the depths, the vertices are pulled from the stack. New numbers are assigned in order of pulling out of the stack.
Color: 3 colors are used during the depth crawl. Initially, all vertices are white. When the top is found, paint it gray. When the list of all vertices adjacent to it is viewed, we paint it black.
I think it will be easier to consider this algorithm by example:

↑ We have an infinite oriented graph. Initially, all the vertices are white, and the stack is empty. Begin the detour from the top of number 1.

Go to the top of number 1. Paint it gray.

↑ There is an edge from vertex number 1 to vertex number 4. Go to vertex number 4 and paint it gray.

↑ There is an edge from vertex number 4 to vertex number 2. Go to vertex number 2 and paint it gray.

↑ From vertex number 2, there are no edges going to black vertices. We return to vertex number 4. We color vertex number 2 in black and put it on the stack.

There is an edge from vertex number 4 to vertex number 3. Go to vertex number 3 and paint it gray.

↑ From vertex number 3 there are no edges going to black vertices. We return to vertex number 4. We color vertex number 3 in black and put it on the stack.

↑ From vertex number 4 there are no edges going to black vertices. We return to vertex number 1. Paint the vertex number 4 in black and put it on the stack.

↑ From vertex number 1, there are no edges going to black vertices. Paint it black and put it on the stack. Point crawl over.

↑ In turn, we get all the vertices from the stack and assign them the numbers 1, 2, 3, 4, respectively. Topology sorting algorithm completed. Graph sorted.
')
Application
Topological sorting is used in a variety of situations, for example, when parallelizing algorithms, when according to some description of the algorithm it is necessary to compile a dependency graph of its operations and, sorting it topologically, determine which of the operations are independent and can be performed in parallel (simultaneously). An example of the use of topological sorting is the creation of a site map, where a tree-like system of sections takes place. (if interested - to google)
As for the implementation - here you can find 22 lines of code implementing this algorithm (everything is carefully commented out)
Source: https://habr.com/ru/post/100953/
All Articles