The MQV protocol is good old Diffie-Hellman, but not quite
For more than 30 years, the Diffie-Hellman key distribution protocol has been pleasing the eye of a simple cryptomaniac for its simplicity and reliability. For those who have spent the last 30 years studying more fun than learning cryptographic protocols, I explain.
The Diffie-Hellman protocol was published in 1976 and marked the beginning of an era of asymmetric cryptography. Its essence is ingeniously simple: Alice and Bob want to get a common key for a symmetric cryptosystem. To do this, they agree, choose two large numbers g and p. These numbers are known to both of them and it makes no sense to keep them secret. Then Alice secretly generates a large secret number a, and Bob - a large number b. And then simple arithmetic takes over. Alice sends Bob the number
 .
.
Bob in turn sends Alice
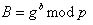 .
.
Now, to get the shared key Alice calculates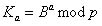 and Bob finds
and Bob finds 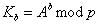 .
.
It is easy to verify that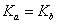 because
because
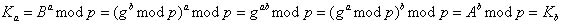 .
.
The genius of the idea is that it will not take long for Alice and Bob to get the key K, while the attacker needs to be able to solve a discrete logarithm problem in order to find K.
Fearing to tire the reader with well-known facts, I turn right to the point. And what if to abstract from the theory and to pass to practice? Then we get the following.
The Diffie-Hellman protocol perfectly opposes a passive attack, but in the case of the “man in the middle” attack, he will not stand. In fact, neither Alice nor Bob can reliably determine who their interlocutor is in the protocol, so it is quite possible to imagine the following situation in which Bob and Alice established contact with Mallory, who Alice impersonating Bob, and Bob appears to be Alice. And then, instead of the Diffie-Hellman protocol, we get something similar to the following:
That is, Mallory gets one key shared with Alice (who believes that this is Bob), and one key shared with Bob (who believes that this is Alice). And, therefore, he can receive from Alice any message for Bob to decrypt him with the key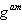 read key encrypt
read key encrypt 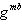 and pass to bob. Thus, forgery can go unnoticed for a very long time.
and pass to bob. Thus, forgery can go unnoticed for a very long time.
')
How to deal with such vulnerabilities? The most logical and simple answer: mutual authentication is needed. And here comes to the aid of digital signature.
If Bob has Alice’s public key and he’s one hundred percent sure that it’s really Alice’s key, then to defend against the man-in-the-middle attack, Alice just needs to sign the number in step 1 with her private key. Now, Mallory can try to pass herself for Alice, but he will not be able to forge her signature, and Bob will immediately begin to be tormented by “vague doubts”.
It would seem that a solution was found, the protocol was improved, the vulnerability was removed. But ... As always, there is one thing. And in this case, the role of such is the excessive increase in the size of messages by adding a signature. The following table demonstrates this effect:
As can be seen from this table, the size of messages increases by several times. It would seem, and God is with them with these extra 320 bits, who will be harmed by them? But in cryptography they do not tolerate half measures. That is why the MQV protocol was devised, which relieves Diffie-Hellman from vulnerability and does not use EDS.
So, the MQV protocol is a key distribution protocol that supports mutual authentication of the parties and thereby eliminates the vulnerability to the man-in-the-middle attack inherent in classic Diffie-Hellman. Among other things, no additional information, like e-signature, is used to authenticate users, which significantly reduces the size of transmitted messages.
Now about the protocol itself.
Alice and Bob each have their own key pair, consisting of public and private keys: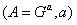 and
and  . Of course, Bob is aware of Alice’s public key, and that, in turn, is Bob’s public key.
. Of course, Bob is aware of Alice’s public key, and that, in turn, is Bob’s public key.
Next, Alice and Bob generate a session key pair: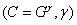 and
and 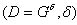 .
.
Then there is an exchange as in the classic Diffie-Hellman protocol:
Alice to Bob: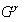
Bob to Alice: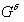
Now Alice knows: A, B, C, D, a , .
.
And Bob is known: A, B, C, D, b ,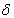 .
.
To get the common key K, they must do the following.
Alice:
Selects the number l equal to the message size in bits divided by 2. So if EC-MQV is used and the message length is 160 bits, then l = 80.
1. Sets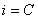
2. Finds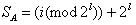
3. Sets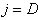
4. Calculates
5. Finds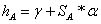
6. Calculates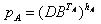
Bob performs the same actions, but with his private keys:
1. Sets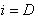
2. Finds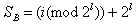
3. Sets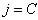
4. Calculates
5. Finds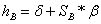
6. Calculates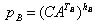
The resulting numbers are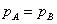 and there is a shared secret key. Make sure of this:
and there is a shared secret key. Make sure of this:
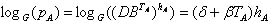 because
because 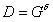 and
and 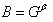 ;
;
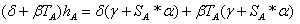 because
because 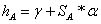 ;
;
 because
because 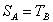 and
and 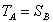 ;
;
 because
because 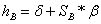 ;
;
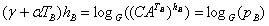 .
.
Note that the transformation keys use the secret keys of both Alice and Bob. Those. Any protocol user can be sure that in addition to the person with whom he wants to establish a connection, no one will be able to get the shared key.
Despite the seeming complexity, the MQV protocol does not lose anything in comparison with the scheme using an EDS, because the same operation of raising to a power modulo a prime number is used both there and there. The benefit of using the protocol is as follows. This is, firstly, resistance to the man-in-the-middle attack, secondly, the small size of messages, and, thirdly, a convenient implementation of the protocol, which saves the user from having to sign each message sent.
upd:
Literature
1. N. Smart "cryptography" (the most complete description of the MQV protocol in Russian from all I have met).
2. Bolotov A. and others. “An elementary introduction to elliptic cryptography” (description of the protocol on elliptic curves).
3. Well, the link to Wikipedia .
The Diffie-Hellman protocol was published in 1976 and marked the beginning of an era of asymmetric cryptography. Its essence is ingeniously simple: Alice and Bob want to get a common key for a symmetric cryptosystem. To do this, they agree, choose two large numbers g and p. These numbers are known to both of them and it makes no sense to keep them secret. Then Alice secretly generates a large secret number a, and Bob - a large number b. And then simple arithmetic takes over. Alice sends Bob the number
 .
.Bob in turn sends Alice
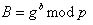 .
.Now, to get the shared key Alice calculates
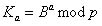 and Bob finds
and Bob finds 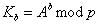 .
.It is easy to verify that
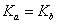 because
because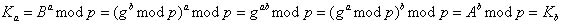 .
.The genius of the idea is that it will not take long for Alice and Bob to get the key K, while the attacker needs to be able to solve a discrete logarithm problem in order to find K.
Fearing to tire the reader with well-known facts, I turn right to the point. And what if to abstract from the theory and to pass to practice? Then we get the following.
The Diffie-Hellman protocol perfectly opposes a passive attack, but in the case of the “man in the middle” attack, he will not stand. In fact, neither Alice nor Bob can reliably determine who their interlocutor is in the protocol, so it is quite possible to imagine the following situation in which Bob and Alice established contact with Mallory, who Alice impersonating Bob, and Bob appears to be Alice. And then, instead of the Diffie-Hellman protocol, we get something similar to the following:
| Step | Alice | Mallory | Bean |
| one | 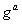  | 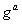 | |
| 2 | 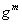  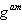 | 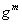 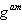 | |
| 3 | 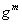  | 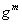 | |
| four | 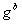  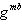 | 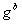 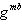 |
That is, Mallory gets one key shared with Alice (who believes that this is Bob), and one key shared with Bob (who believes that this is Alice). And, therefore, he can receive from Alice any message for Bob to decrypt him with the key
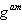 read key encrypt
read key encrypt 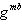 and pass to bob. Thus, forgery can go unnoticed for a very long time.
and pass to bob. Thus, forgery can go unnoticed for a very long time.')
EDS as protection
How to deal with such vulnerabilities? The most logical and simple answer: mutual authentication is needed. And here comes to the aid of digital signature.
If Bob has Alice’s public key and he’s one hundred percent sure that it’s really Alice’s key, then to defend against the man-in-the-middle attack, Alice just needs to sign the number in step 1 with her private key. Now, Mallory can try to pass herself for Alice, but he will not be able to forge her signature, and Bob will immediately begin to be tormented by “vague doubts”.
It would seem that a solution was found, the protocol was improved, the vulnerability was removed. But ... As always, there is one thing. And in this case, the role of such is the excessive increase in the size of messages by adding a signature. The following table demonstrates this effect:
| Algorithms | Message size | Signature size | Overall size |
| Diffie-Hellman + DSA-signature | 1024 bits | 320 bits | 1344 bits |
| Diffie-Hellman + RSA-signature | 1024 | 1024 | 2048 |
| Diffie-Hellman (on elliptic curves) + RSA-signature | 160 | 1024 | 1184 |
| Diffie-Hellman (on elliptic curves) + DSA-signature (on elliptic curves) | 160 | 320 | 480 |
As can be seen from this table, the size of messages increases by several times. It would seem, and God is with them with these extra 320 bits, who will be harmed by them? But in cryptography they do not tolerate half measures. That is why the MQV protocol was devised, which relieves Diffie-Hellman from vulnerability and does not use EDS.
MQV protocol
So, the MQV protocol is a key distribution protocol that supports mutual authentication of the parties and thereby eliminates the vulnerability to the man-in-the-middle attack inherent in classic Diffie-Hellman. Among other things, no additional information, like e-signature, is used to authenticate users, which significantly reduces the size of transmitted messages.
| Protocol | Message size |
| Mqv | 1024 bits |
| MQV (on elliptic curves) | 160 bits |
Now about the protocol itself.
Alice and Bob each have their own key pair, consisting of public and private keys:
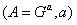 and
and  . Of course, Bob is aware of Alice’s public key, and that, in turn, is Bob’s public key.
. Of course, Bob is aware of Alice’s public key, and that, in turn, is Bob’s public key.Next, Alice and Bob generate a session key pair:
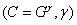 and
and 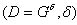 .
.Then there is an exchange as in the classic Diffie-Hellman protocol:
Alice to Bob:
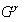
Bob to Alice:
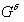
Now Alice knows: A, B, C, D, a ,
 .
.And Bob is known: A, B, C, D, b ,
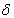 .
.To get the common key K, they must do the following.
Alice:
Selects the number l equal to the message size in bits divided by 2. So if EC-MQV is used and the message length is 160 bits, then l = 80.
1. Sets
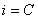
2. Finds
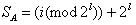
3. Sets
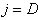
4. Calculates

5. Finds
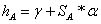
6. Calculates
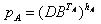
Bob performs the same actions, but with his private keys:
1. Sets
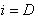
2. Finds
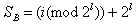
3. Sets
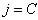
4. Calculates

5. Finds
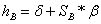
6. Calculates
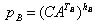
The resulting numbers are
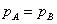 and there is a shared secret key. Make sure of this:
and there is a shared secret key. Make sure of this: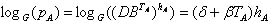 because
because 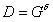 and
and 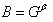 ;
;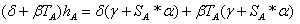 because
because 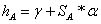 ;
; because
because 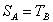 and
and 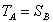 ;
; because
because 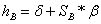 ;
;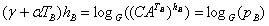 .
.Note that the transformation keys use the secret keys of both Alice and Bob. Those. Any protocol user can be sure that in addition to the person with whom he wants to establish a connection, no one will be able to get the shared key.
Despite the seeming complexity, the MQV protocol does not lose anything in comparison with the scheme using an EDS, because the same operation of raising to a power modulo a prime number is used both there and there. The benefit of using the protocol is as follows. This is, firstly, resistance to the man-in-the-middle attack, secondly, the small size of messages, and, thirdly, a convenient implementation of the protocol, which saves the user from having to sign each message sent.
upd:
Literature
1. N. Smart "cryptography" (the most complete description of the MQV protocol in Russian from all I have met).
2. Bolotov A. and others. “An elementary introduction to elliptic cryptography” (description of the protocol on elliptic curves).
3. Well, the link to Wikipedia .
Source: https://habr.com/ru/post/100950/
All Articles