Cryptographic strength 1000-fold password hashing

The discussion about the cryptographic strength of repeated use of a hash over a password (which slipped, by the way, in other forums), which has risen in this topic , pushed me to this somewhat mathematical topic. The essence of the problem arises from the idea of ​​repeatedly (1,000 or more times) processing a password before storing with any crypto-resistant algorithm (most often a hash function) in order to get a slow verification algorithm, thereby effectively opposing brute force in case of an interception or theft values. As hrat users of Scratch (the author of the first article), mrThe and IlyaPodkopaev quite rightly noted, the idea is not new and developers of the equipment of Cisco, the RAR archiver and many others use it. But, since hashing is an operation that compresses a set of values, a completely natural question arises - will we not harm the stability of the system? Attempt to answer this question -

Reduction of resilience will be considered in two threat models:

1. the attacker bans random input byte sets in the hope of finding a collision due to the narrowing of the value space (“full brute force”);
2. bust through the dictionary.

Let's start with the first, more theoretical, question: “can such a huge space of values ​​of a modern hash function ^2,128 (MD5), 2,160 (SHA-1), ^2,256 (GOST R 34.11, SHA-256) narrow as a result of repeated use to the extent that a collision with it can be picked up by a simple random search? ”
')

Start

One of the main properties / requirements for crypto-resistant hash functions is a very good uniformity of distribution of output results. This makes it possible to operate in the estimates required by ordinary probability theory and combinatorics.

Let us take an input set of N elements and, in the output set, also of N objects, randomly assign an element to each of its objects (see the figure). It is obvious that several mappings will be shown on identical elements, and, therefore, there will be elements that are not matched by any arrows:



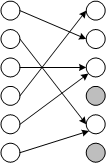
The probability that a particular element of the output set will NOT be chosen by a specific display (arrow) is equal to 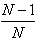accordingly, the probability that it will NOT be selected by any of the N arrows is equal to or what is the same (thanks to the property of crypto-resistant hash function, all N mappings are independent events in the first approximation).

Limit is a consequence of the second remarkable limit and is equal to i.e. approximately 0.3679. This is the probability that the element in the output set will "turn gray." At the same time, we note that for large N (greater than 2 ³² ) the degree of “degradation” does not depend on the digit capacity of the hash function. As a result, after the first repetition of hashing, only about 63% will remain from the value space. If everything goes further, it will be a catastrophe - in only 150 iterations we will “eat” 100 bits of the output space, leaving, for example, for MD5 only ^2,128-100 = 2 ²⁸ options. Fortunately, it is not.

In detail

As soon as the input set begins to be filled out completely (that is, after the second iteration in the first threat model or immediately in the second threat model (with a dictionary attack)), other formulas and other patterns begin to work. This is clearly seen in the same figure for the case if there were only 3 “active” elements in the input set. The probability of “losing” an element (narrowing the output set) decreases sharply, since now far less often two or more mappings are found on the same element.



Let only kN elements be active in the input set, where 0 <k <1 . Then the probability of not choosing a particular element is 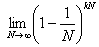that by the same consequence , and the narrowing of the output set on this iteration will be only . Here is a table of the first 6 iterations:

Iteration number, i	The proportion of the set of values, k
one	1.0000
2	0.6321
3	0.4685
four	0.3740
five	0.3120
6	0.2680

Of course, the share of active elements continues to decrease with each iteration, but not as quickly and catastrophically as at the very beginning.

In order to assess the degree of reduction of resistance for a large number of iterations, it is more convenient to study not the number k itself, but the opposite to it — how many times the output set has been reduced, and right away on the base 2 log scale, so that the units of measurement are bits: . It is this number that will characterize the reduction in the resistance to full enumeration - it must be subtracted from the bit width of the selected hash function in order to get the bit depth equivalent to the stable hash function. The graph of r up to 50.000 iterations is shown in the figure: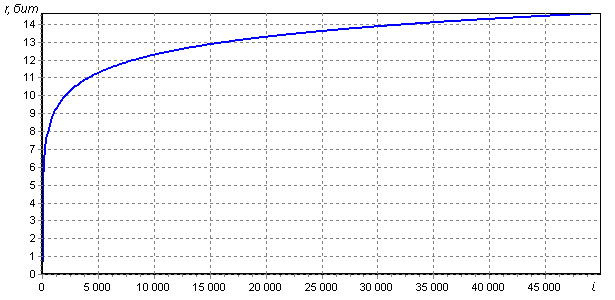



The points at which the graph intersects the integer values ​​of r are summarized in the table:

Reduced durability r (bit)	Number of iterations, i
four	thirty
five	61
6	125
7	253
eight	509
9	1.020
ten	2.044
eleven	4.092
12	8.188
13	16.379
14	32.763
15	65.531
sixteen	131.067
...	...
20	2.097.146
...	...
24	33.554.425

As you can see, the decrease in durability from a certain point increases very slowly. Moreover, the number of iterations exactly follows the powers of two: . In all cases when similar patterns are observed, they can be proved analytically, but I did not set it as my goal. Thus, without reducing the robustness of the algorithm to more than 16 bits (and in my firm conviction for 128-bit hash functions, this does not affect their practical strength for the next 25 years, for example), you can perform 130.000 password hash iterations. For 256-bit hash functions (SHA-256, GOST R 34.11, RIPEMD-256, etc.), obviously, this bar is still many times higher.

Validation of the model

As always, after a large number of theoretical speculations, there is a desire to at least somehow assess how far the obtained theory is from practice. As a test hash function, I took the first 16 bits from MD5 (a crypto-resistant hash function allows you to select any set of result bits to form a truncated hash function with similar properties, although, of course, less persistence - according to its new bit depth). All possible values ​​from 0 to 0xFFFF are input to the algorithm, i iterations are performed over each of the values, each iteration consists in calculating the first 16 bits of the MD5 result (a 16-bit hash function is obtained). "The results of the experiments" are given in the table:

Planned decrease in durability, r (bit)	Number of iterations, i	The expected number of elements in the set	The observed number of elements in the set
four	thirty	2 16-4 = 4.096	3.819
6	125	2 16-6 = 1.024	831
eight	509	2 16-8 = 256	244

Of course, with such a small value of N and especially kN , the fact that all the calculations above are given for limits (for N comparable and large ^2,128 , everything is good) is immediately apparent. But even here, the general trend is traced and acceptably fit into the formulas obtained above.

Corollary - resistance to dictionary attack

The time has come to analyze whether “the narrowing of the range of meanings is perceptible in those cases when a vocabulary or easily constructed password is chosen as a passphrase?” . Obviously, in this case the “active” input set of values ​​is already extremely narrowed - it depends on the selection methods in the range from 2 ¹⁶ to 2 ⁴⁸ . Thus, we immediately find ourselves in a “discharged” situation - in the right side of the graph. Here, the probability of displaying two different input elements on the same output is extremely small. Millions and millions of operations practically do not change the number of elements in the output set at all. Units / tens are eliminated - there is no question of any practical reduction in the persistence of speech.

findings

The described scheme of protection against brute force can be freely applied in practice with virtually no restrictions on the part of cryptographic security. The recommended upper limits for the number of iterations (the allowed decrease in the stability of r is chosen subjectively in the amount ^of _1/8 digits of the hash function) are given in the table:

Hash function bit (bits)	Permitted decrease in durability, r (bit)	The upper limit of the allowed number of iterations, i
128	sixteen	130.000
160	20	2,000,000
192	24	32.000.000
224	28	500.000.000
256	32	8.000.000.000