What is supersymmetry?
The Large Hadron Collider (LHC) has already begun its work. Its launch aroused considerable interest and was accompanied by a large number of diverse and, at times, anti-scientific rumors and speculations.
One of the important goals of the LHC is to test supersymmetric models. Supersymmetry is just an area of my scientific activity, and I decided to try in a scientific form to try to tell what it is.
I will focus in this article on modern theories of elementary particle physics, on some ideas and consequences of these theories. Among the topics covered are the following:
')
The physics of elementary particles is one of the few areas of human knowledge where it was possible to penetrate deeper into the secrets of matter and explain its properties. Until now, the reduction in the number of laws describing the world has been one of the main trends in the construction of scientific theories. In this case, the main goal has always remained and remains the construction of a unified field theory, which would unite all knowledge of mankind about nature, and from which one could derive (at least in principle) all laws as particular cases of such a theory.
Currently, there are four fundamental interactions: gravitational , electromagnetic , strong and weak . The first two have long-range effects and are manifested in everyday life. Gravity, for example, controls the movement of celestial bodies. We all experience the gravitational pull of the Earth. Electromagnetism explains most of the phenomena that a person faces in everyday life. The other two interactions are short-range. They appear only on the scale of the atomic nucleus (explain alpha and beta decay) and become decisive on smaller scales.
In the microcosm, the quantum properties of particles play a key role. To describe the fundamental interactions, however, ordinary quantum mechanics is not enough. Firstly, quantum mechanics is a non-relativistic theory, that is, it is true for low speeds compared to the speed of light. Secondly, quantum mechanics does not describe the processes of birth and destruction of particles that occur during the interaction of high-energy particles. Relativistic generalization (consistent with the ideas of the special theory of relativity) of quantum mechanics is quantum field theory .
In quantum field theories, particles of matter are “quanta” (perturbations) of the corresponding fields. The interaction between particles is transferred by special fields. It is assumed that particles of matter in the process of interaction emit and absorb other particles - the quanta of the field-carrier.
The first successful example of quantum field theory - quantum electrodynamics - was built in the works of Feynman, Schwinger and Tomonagi in the mid-twentieth century, for which they were awarded the Nobel Prize in 1965. Quantum electrodynamics considers the interaction between charged particles (for example, electrons and positrons), arising from the exchange of photons - quanta of the electromagnetic field.
Until now, quantum electrodynamics remains the most accurate physical theory. The theoretical calculations in the framework of quantum electrodynamics coincide with the experimental results with an accuracy of up to 10 −10 .
By symmetry, physicists understand the immutability of something when performing certain transformations. In this case, an important role is played by the symmetry of laws , or equations . For example, the equation x 2 = 4 is symmetric (that is, it does not change) with respect to the transformation x → −x .
In the physics of symmetry play a dual role. First, each type of symmetry of a physical system corresponds to a conserved quantity. For example, from the homogeneity of time (unchanged with respect to transformations t → t + Δt ) follows the energy conservation law, from the homogeneity of space (unchanged with respect to coordinate transformations x → x + Δx ) - the law of conservation of momentum, from the isotropy of space (unchanged with respect to turns) - the law of conservation angular momentum (angular momentum L = mvr characterizes the “amount of rotation” and is analogous to the momentum p = mv ).
Secondly, it is possible to require the fulfillment of various symmetries from new physical theories. The more such requirements - the less arbitrariness in the construction of the theory.
An example of a physical theory with symmetry is ordinary quantum mechanics, which operates with wave functions. The wave function of a particle is a complex function, for example, spatial coordinates (roughly speaking, a complex number at each point). It can be calculated from the Schrödinger equation. Physical meaning is not the wave function itself, but the square of its modulus, which shows the probability of a particle being in some place.
If all wave functions are multiplied by the same complex number with module 1, no theoretical predictions will change. Indeed, the modulus of a product of complex numbers is equal to the product of modules, and no such probabilities change from such a multiplication.
This is an example of the so-called global symmetry (global - because the wave function multiplied at different points by the same number). The essence of this symmetry is that the theory does not change with respect to a certain class of transformations (in our case, these transformations are multiplication by an arbitrary complex number with a modulus of 1).
Quantum electrodynamics has symmetry with respect to transformations, called gauge . These transformations consist in multiplying the field of electrons by a complex number with module 1 (although in order for the theory not to change, several other transformations of the electromagnetic field must be performed simultaneously with the conversion of the field of electrons). In contrast to the case of quantum mechanics considered above, this number may already be different at each point (local symmetry).
It is interesting to note the next moment. As mentioned above, a conserved quantity is associated with each symmetry. In the case of gauge transformations of quantum electrodynamics, such a conserved quantity is the usual electric charge.
In the fifties, Yang and Mills built a model whose equations did not change under the influence of more complex local gauge transformations. At first the interest was purely mathematical. However, later, on the basis of the Yang-Mills theory, the main theories of the interaction of elementary particles were created — the theory of electroweak interactions and quantum chromodynamics. These theories with gauge symmetry have been experimentally verified.
In the sixties, it was possible to combine electromagnetism and weak interactions. Salam, Glashow and Weinberg built a theory of electroweak interactions. In 1979, they were awarded the Nobel Prize. The new theory predicted the existence of new particles, the so-called W and Z bosons. They are responsible for the "transfer" of weak interaction. These bosons were discovered on a proton supersinhrotron in 1983.
It would seem, how can electromagnetic and weak interactions be combined if the first have a radius of interaction that is infinite (indeed, we see light - electromagnetic radiation - from distant galaxies and other astronomical objects), and in the second it does not exceed the size of the atomic nucleus? It turns out that this “asymmetry” is due to the fact that the mass of photons is zero, and the mass of the W and Z bosons is very large, they are about 100 times heavier than a proton.
The violation of the so-called electroweak symmetry is an important property of the theory of electroweak interactions (the equations of the theory have this symmetry). As a result of the violation, the W and Z bosons and some other particles (for example, electrons) acquire masses.
In the framework of the Yang-Mills model, the gauge bosons cannot be made massive without destroying the gauge symmetry. To break the electroweak symmetry, the Higgs mechanism was invented. The basic idea is that the whole space permeates a special Higgs field, which interacts with the other fields and violates symmetry, although the equations of the theory remain symmetrical. The perturbations of the Higgs field should appear in the experiment as new particles — the Higgs bosons. The Higgs boson is a very heavy particle, heavier than the W and Z bosons. Therefore, it is not yet open experimentally.
The theory of strong interactions, quantum chromodynamics , is also based on the Yang-Mills equations. Quantum chromodynamics says that many elementary particles - mesons and baryons (for example, a proton) - are composed of quarks. However, isolated quarks have never been observed (this phenomenon is called confinement ). Due to the complexity of the equations of quantum chromodynamics, confinement has not yet been derived directly from them. By the way, solving the Yang-Mills equations and explaining confinement is one of the seven millennium problems for which the Clay Institute awarded a million dollar prize.
Quantum chromodynamics is also confirmed in accelerator experiments. The standard model of fundamental interactions includes the model of electroweak interactions and quantum chromodynamics. The standard model was able to explain almost all the experimental data obtained so far in elementary particle physics.
Before proceeding to the discussion of supersymmetry, consider the concept of spin . Spin is its own angular momentum inherent in each particle. It is measured in units of Planck’s constant and is whole or half-integer. Spin is a purely quantum-mechanical property; it cannot be represented from the classical point of view. A naive attempt to treat elementary particles as small “balls”, and spin - as their rotation, contradicts the special theory of relativity, since the points on the surface of the balls should then move faster than light. Electrons have spin 1/2, photons spin 1.
Supersymmetry is symmetry between particles with whole and half-integer spins. The idea of supersymmetry was proposed in the theoretical works of Golfand and Likhtman, Volkov and Akulov, as well as Wess and Zumino about 40 years ago. In short, it consists in constructing theories whose equations would not change when converting fields with integer spin into fields with half-integer spin and vice versa. Since then, thousands of articles have been written, all models of quantum field theory have been subjected to supersymmetrization, and a new mathematical apparatus has been developed, which allows us to construct supersymmetric theories.
The standard model of fundamental interactions discussed earlier can also be made supersymmetric. At the same time, a number of its problems are solved. Consider some of them.
Despite the huge successes of the Standard Model in explaining experimental data, it has a number of theoretical difficulties that do not allow the Standard Model to be the ultimate theory describing our world. It turns out that some of these difficulties can be overcome with a supersymmetric extension of the Standard Model.
The hypothesis of the great unification that many physicists adhere to says that various fundamental interactions are manifestations of one, more general, interaction. This interaction should manifest itself at enormous energies (according to various estimates, the energy of a great union is 10 13 or even 10 16 times greater than the energy available to modern accelerators of elementary particles). When the energy decreases, the gravitational interaction splits off from the combined interaction, then the strong interaction, and finally, the electroweak interaction splits into the weak and electromagnetic interaction.
In the Standard Model, however, the electro-weak and strong interactions are only formally combined. They may turn out to be different manifestations of a general interaction, or they may not. Nevertheless, an analysis of the experimental results gives some clues to the question of the existence of a great union.
Each of the fundamental interactions has a value that characterizes its intensity. This value is called the interaction constant . The constant of electromagnetic interactions is simply equal to the electron charge. In the case of strong and weak interactions, the situation is somewhat more complicated.
One of the interesting properties of quantum field theory is that the interaction constant is not really a constant — it changes as the characteristic energies of processes involving elementary particles change, and the theory can predict the nature of this dependence.
In particular, this means that when approaching an electron at distances much smaller than the size of an atom, its charge begins to change! Moreover, such a change due to quantum effects is confirmed by experimental data, for example, by a small change in the energy levels of electrons in a hydrogen atom (Lamb shift).
The constants of electromagnetic, weak, and strong interactions are measured with sufficient accuracy so that their change with energy can be calculated. The results are shown in the figure. In the Standard Model (graphics on the left) there are no such energies where the coupling of the interaction constants would occur. And in the minimal supersymmetric expansion of the Standard Model (graphics on the right) there is such a point. This means that supersymmetry in the physics of elementary particles has a pleasant property — a great unification is possible within its framework!
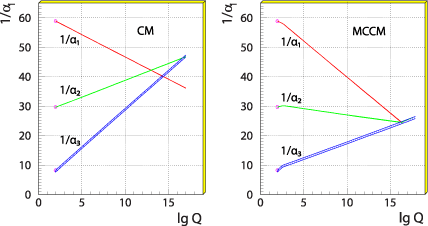
The evolution of gauge coupling constants with increasing energy scale in the Standard Model and MSSM.
The standard model does not include gravitational interaction. It is completely unnoticeable in accelerator experiments due to the small masses of elementary particles. However, at high energies, gravity can become substantial.
The modern theory of gravitational interactions - the general theory of relativity - is a classical theory. A quantum generalization of this theory would undoubtedly become the most general physical theory if it were constructed. In addition to the absence of any experimental data, there are serious theoretical obstacles in the construction of the theory of quantum gravity.
There are also difficulties in combining gravity with the rest of the interactions. The gravitational interaction carrier, the graviton, must have spin 2, while the carrier spin of the other interactions (photon, W and Z bosons, gluons) is 1. To “mix” these fields, you need a transformation that changes the spin. And the transformation of supersymmetry is just such a transformation. It reduces the spin of a particle by 1/2 and, therefore, can mix particles with different spins. Thus, combining with gravity within supersymmetry is quite natural.
Supersymmetry may explain some of the results of research in cosmology. One of these results is that the visible (luminous) matter does not constitute all the matter in the Universe. A significant amount of energy comes from so-called dark matter and dark energy .
Direct evidence for the existence of dark matter is the dependence of the velocities of stars in spiral galaxies on their distance from the center. This dependence is easy to calculate. It turns out that the experimental data significantly differ from the predictions of the theory.
The discrepancy is explained by the fact that galaxies are in the "clouds" of dark matter. Dark matter particles interact only gravitationally. Therefore, they are grouped around galaxies (it would be more correct to say that ordinary matter is grouped around clumps of dark matter) and distort the mass distribution in the galaxy.
Relic radiation - the equilibrium thermal radiation filling the Universe. This radiation was separated from matter in the early stages of the expansion of the Universe, when electrons combined with protons and formed hydrogen atoms (recombination). Then the universe was 1000 times younger than it is now. The current temperature of the CMB is about 3 K.
Recent high-precision measurements of the temperature distribution of the CMB across the sky in the WMAP experiment showed that the total energy of the Universe is distributed between dark energy (73%), dark matter (23%) and ordinary matter (4%), that is, dark matter is a significant part, exceeding many times the proportion of visible matter.
There are no suitable particles in the Standard Model to explain dark matter. At the same time, in some supersymmetric models there is an excellent candidate for the role of cold dark matter, namely neutralino, the lightest supersymmetric particle. It is stable, so that relic neutralinos could persist in the Universe from the time of the Big Bang.
As for dark energy, its nature in the framework of modern physical theories is completely incomprehensible. This is a real challenge to the physicists of the twenty-first century. Dark energy can be interpreted as the self-energy of a vacuum, however, there are huge discrepancies between the theoretical estimates and the observed value of the density of dark energy. The existence of dark energy leads to observable consequences - accelerated expansion of the Universe at the present time.
To build supersymmetric models, a mathematical apparatus was developed, to dwell on which there is no possibility. However, despite the complexity of the mathematical apparatus, supersymmetric theories have a number of simple features.
One of these features is the doubling of the number of particles. Each particle acquires a super-partner — a particle that has exactly the same properties, with the exception of the spin, which differs by 1/2.
In the Standard Model, there are no particles that could be each other's superpartners. Consequently, in the supersymmetric extensions of the Standard Model, each particle acquires its own super-partner — a new particle. The minimal supersymmetric Standard Model (MSSM) requires the least new particles to build.
Another important feature of supersymmetric models is the violation of supersymmetry. If there was no such violation, the superpartners would have the same mass as ordinary particles. However, new particles with masses of known particles of the Standard Model have never been observed. Also without the breaking of supersymmetry, the Higgs mechanism of breaking the electroweak symmetry would not work.
To apply supersymmetric models in high-energy physics, it is necessary to require a violation of supersymmetry. In this case, superpartners can acquire large masses, which can explain their non-observation at the present time.
The specific mechanism for breaking supersymmetry is currently unknown. This significantly reduces the predictive power of the model, since a large number of free parameters appear in it, choosing which one can get arbitrary consequences. Some considerations, such as the grand unification hypothesis, allow us to limit the number of free parameters. The study of restrictions on the parameters of supersymmetric models is one of the important directions in the study of physics beyond the Standard Model.
Supersymmetry is one of the main candidates for the role of a new theory in elementary particle physics beyond the framework of the Standard Model. The search for various manifestations of supersymmetry in nature has been one of the main objectives of numerous experiments at colliders (LEP - large electron-positron collider and Tevatron) and in non-accelerator experiments for several decades.
Unfortunately, the result is still negative. There are no direct indications of the existence of supersymmetry in particle physics, although the available supersymmetric models in general are not prohibited by the existing theoretical and experimental requirements.
LHC (Large Hadron Collider) is a new accelerator built at CERN. His energy is seven times the energy of the current American accelerator Tevatron. In most supersymmetric models, the masses of new particles lie in the region accessible by the LHC. It is assumed that the Higgs boson and supersymmetric particles will be discovered at the LHC. In new experiments, low-energy supersymmetry will be either detected or excluded.
Although supersymmetry is not open to experience, various supersymmetric models can be investigated now. First, it is necessary to exclude models in which new particles have insufficiently large masses, which have now been experimentally closed. Secondly, discrepancies between some experimental data and theoretical predictions of the Standard Model can be explained by the contribution of supersymmetric particles, and from this point of view some supersymmetric models are preferable to others.
Many specialists in high energy physics are exploring various options for supersymmetric models and their consequences. It is possible that one of these models will be confirmed on the LHC accelerator.
One of the important goals of the LHC is to test supersymmetric models. Supersymmetry is just an area of my scientific activity, and I decided to try in a scientific form to try to tell what it is.
I will focus in this article on modern theories of elementary particle physics, on some ideas and consequences of these theories. Among the topics covered are the following:
- The standard model of fundamental interactions (describes almost all the experimental data in particle physics),
- its strengths and weaknesses
- the idea of supersymmetry,
- solution of many problems of the Standard Model with its supersymmetric generalization,
- some features of the minimal supersymmetric Standard Model (MSSM),
- experimental supersymmetry status.
')
Theoretical foundations of elementary particle physics
The physics of elementary particles is one of the few areas of human knowledge where it was possible to penetrate deeper into the secrets of matter and explain its properties. Until now, the reduction in the number of laws describing the world has been one of the main trends in the construction of scientific theories. In this case, the main goal has always remained and remains the construction of a unified field theory, which would unite all knowledge of mankind about nature, and from which one could derive (at least in principle) all laws as particular cases of such a theory.
Fundamental interactions
Currently, there are four fundamental interactions: gravitational , electromagnetic , strong and weak . The first two have long-range effects and are manifested in everyday life. Gravity, for example, controls the movement of celestial bodies. We all experience the gravitational pull of the Earth. Electromagnetism explains most of the phenomena that a person faces in everyday life. The other two interactions are short-range. They appear only on the scale of the atomic nucleus (explain alpha and beta decay) and become decisive on smaller scales.
In the microcosm, the quantum properties of particles play a key role. To describe the fundamental interactions, however, ordinary quantum mechanics is not enough. Firstly, quantum mechanics is a non-relativistic theory, that is, it is true for low speeds compared to the speed of light. Secondly, quantum mechanics does not describe the processes of birth and destruction of particles that occur during the interaction of high-energy particles. Relativistic generalization (consistent with the ideas of the special theory of relativity) of quantum mechanics is quantum field theory .
Quantum field theory
In quantum field theories, particles of matter are “quanta” (perturbations) of the corresponding fields. The interaction between particles is transferred by special fields. It is assumed that particles of matter in the process of interaction emit and absorb other particles - the quanta of the field-carrier.
The first successful example of quantum field theory - quantum electrodynamics - was built in the works of Feynman, Schwinger and Tomonagi in the mid-twentieth century, for which they were awarded the Nobel Prize in 1965. Quantum electrodynamics considers the interaction between charged particles (for example, electrons and positrons), arising from the exchange of photons - quanta of the electromagnetic field.
Until now, quantum electrodynamics remains the most accurate physical theory. The theoretical calculations in the framework of quantum electrodynamics coincide with the experimental results with an accuracy of up to 10 −10 .
Symmetry in elementary particle physics
By symmetry, physicists understand the immutability of something when performing certain transformations. In this case, an important role is played by the symmetry of laws , or equations . For example, the equation x 2 = 4 is symmetric (that is, it does not change) with respect to the transformation x → −x .
In the physics of symmetry play a dual role. First, each type of symmetry of a physical system corresponds to a conserved quantity. For example, from the homogeneity of time (unchanged with respect to transformations t → t + Δt ) follows the energy conservation law, from the homogeneity of space (unchanged with respect to coordinate transformations x → x + Δx ) - the law of conservation of momentum, from the isotropy of space (unchanged with respect to turns) - the law of conservation angular momentum (angular momentum L = mvr characterizes the “amount of rotation” and is analogous to the momentum p = mv ).
Secondly, it is possible to require the fulfillment of various symmetries from new physical theories. The more such requirements - the less arbitrariness in the construction of the theory.
An example of a physical theory with symmetry is ordinary quantum mechanics, which operates with wave functions. The wave function of a particle is a complex function, for example, spatial coordinates (roughly speaking, a complex number at each point). It can be calculated from the Schrödinger equation. Physical meaning is not the wave function itself, but the square of its modulus, which shows the probability of a particle being in some place.
If all wave functions are multiplied by the same complex number with module 1, no theoretical predictions will change. Indeed, the modulus of a product of complex numbers is equal to the product of modules, and no such probabilities change from such a multiplication.
This is an example of the so-called global symmetry (global - because the wave function multiplied at different points by the same number). The essence of this symmetry is that the theory does not change with respect to a certain class of transformations (in our case, these transformations are multiplication by an arbitrary complex number with a modulus of 1).
Quantum electrodynamics has symmetry with respect to transformations, called gauge . These transformations consist in multiplying the field of electrons by a complex number with module 1 (although in order for the theory not to change, several other transformations of the electromagnetic field must be performed simultaneously with the conversion of the field of electrons). In contrast to the case of quantum mechanics considered above, this number may already be different at each point (local symmetry).
It is interesting to note the next moment. As mentioned above, a conserved quantity is associated with each symmetry. In the case of gauge transformations of quantum electrodynamics, such a conserved quantity is the usual electric charge.
In the fifties, Yang and Mills built a model whose equations did not change under the influence of more complex local gauge transformations. At first the interest was purely mathematical. However, later, on the basis of the Yang-Mills theory, the main theories of the interaction of elementary particles were created — the theory of electroweak interactions and quantum chromodynamics. These theories with gauge symmetry have been experimentally verified.
Standard Model of Fundamental Interactions
In the sixties, it was possible to combine electromagnetism and weak interactions. Salam, Glashow and Weinberg built a theory of electroweak interactions. In 1979, they were awarded the Nobel Prize. The new theory predicted the existence of new particles, the so-called W and Z bosons. They are responsible for the "transfer" of weak interaction. These bosons were discovered on a proton supersinhrotron in 1983.
It would seem, how can electromagnetic and weak interactions be combined if the first have a radius of interaction that is infinite (indeed, we see light - electromagnetic radiation - from distant galaxies and other astronomical objects), and in the second it does not exceed the size of the atomic nucleus? It turns out that this “asymmetry” is due to the fact that the mass of photons is zero, and the mass of the W and Z bosons is very large, they are about 100 times heavier than a proton.
The violation of the so-called electroweak symmetry is an important property of the theory of electroweak interactions (the equations of the theory have this symmetry). As a result of the violation, the W and Z bosons and some other particles (for example, electrons) acquire masses.
In the framework of the Yang-Mills model, the gauge bosons cannot be made massive without destroying the gauge symmetry. To break the electroweak symmetry, the Higgs mechanism was invented. The basic idea is that the whole space permeates a special Higgs field, which interacts with the other fields and violates symmetry, although the equations of the theory remain symmetrical. The perturbations of the Higgs field should appear in the experiment as new particles — the Higgs bosons. The Higgs boson is a very heavy particle, heavier than the W and Z bosons. Therefore, it is not yet open experimentally.
The theory of strong interactions, quantum chromodynamics , is also based on the Yang-Mills equations. Quantum chromodynamics says that many elementary particles - mesons and baryons (for example, a proton) - are composed of quarks. However, isolated quarks have never been observed (this phenomenon is called confinement ). Due to the complexity of the equations of quantum chromodynamics, confinement has not yet been derived directly from them. By the way, solving the Yang-Mills equations and explaining confinement is one of the seven millennium problems for which the Clay Institute awarded a million dollar prize.
Quantum chromodynamics is also confirmed in accelerator experiments. The standard model of fundamental interactions includes the model of electroweak interactions and quantum chromodynamics. The standard model was able to explain almost all the experimental data obtained so far in elementary particle physics.
Supersymmetry
The idea of supersymmetry
Before proceeding to the discussion of supersymmetry, consider the concept of spin . Spin is its own angular momentum inherent in each particle. It is measured in units of Planck’s constant and is whole or half-integer. Spin is a purely quantum-mechanical property; it cannot be represented from the classical point of view. A naive attempt to treat elementary particles as small “balls”, and spin - as their rotation, contradicts the special theory of relativity, since the points on the surface of the balls should then move faster than light. Electrons have spin 1/2, photons spin 1.
Supersymmetry is symmetry between particles with whole and half-integer spins. The idea of supersymmetry was proposed in the theoretical works of Golfand and Likhtman, Volkov and Akulov, as well as Wess and Zumino about 40 years ago. In short, it consists in constructing theories whose equations would not change when converting fields with integer spin into fields with half-integer spin and vice versa. Since then, thousands of articles have been written, all models of quantum field theory have been subjected to supersymmetrization, and a new mathematical apparatus has been developed, which allows us to construct supersymmetric theories.
The standard model of fundamental interactions discussed earlier can also be made supersymmetric. At the same time, a number of its problems are solved. Consider some of them.
Supersymmetry motivation
Despite the huge successes of the Standard Model in explaining experimental data, it has a number of theoretical difficulties that do not allow the Standard Model to be the ultimate theory describing our world. It turns out that some of these difficulties can be overcome with a supersymmetric extension of the Standard Model.
Union of coupling constants
The hypothesis of the great unification that many physicists adhere to says that various fundamental interactions are manifestations of one, more general, interaction. This interaction should manifest itself at enormous energies (according to various estimates, the energy of a great union is 10 13 or even 10 16 times greater than the energy available to modern accelerators of elementary particles). When the energy decreases, the gravitational interaction splits off from the combined interaction, then the strong interaction, and finally, the electroweak interaction splits into the weak and electromagnetic interaction.
In the Standard Model, however, the electro-weak and strong interactions are only formally combined. They may turn out to be different manifestations of a general interaction, or they may not. Nevertheless, an analysis of the experimental results gives some clues to the question of the existence of a great union.
Each of the fundamental interactions has a value that characterizes its intensity. This value is called the interaction constant . The constant of electromagnetic interactions is simply equal to the electron charge. In the case of strong and weak interactions, the situation is somewhat more complicated.
One of the interesting properties of quantum field theory is that the interaction constant is not really a constant — it changes as the characteristic energies of processes involving elementary particles change, and the theory can predict the nature of this dependence.
In particular, this means that when approaching an electron at distances much smaller than the size of an atom, its charge begins to change! Moreover, such a change due to quantum effects is confirmed by experimental data, for example, by a small change in the energy levels of electrons in a hydrogen atom (Lamb shift).
The constants of electromagnetic, weak, and strong interactions are measured with sufficient accuracy so that their change with energy can be calculated. The results are shown in the figure. In the Standard Model (graphics on the left) there are no such energies where the coupling of the interaction constants would occur. And in the minimal supersymmetric expansion of the Standard Model (graphics on the right) there is such a point. This means that supersymmetry in the physics of elementary particles has a pleasant property — a great unification is possible within its framework!

The evolution of gauge coupling constants with increasing energy scale in the Standard Model and MSSM.
Combining with gravity
The standard model does not include gravitational interaction. It is completely unnoticeable in accelerator experiments due to the small masses of elementary particles. However, at high energies, gravity can become substantial.
The modern theory of gravitational interactions - the general theory of relativity - is a classical theory. A quantum generalization of this theory would undoubtedly become the most general physical theory if it were constructed. In addition to the absence of any experimental data, there are serious theoretical obstacles in the construction of the theory of quantum gravity.
There are also difficulties in combining gravity with the rest of the interactions. The gravitational interaction carrier, the graviton, must have spin 2, while the carrier spin of the other interactions (photon, W and Z bosons, gluons) is 1. To “mix” these fields, you need a transformation that changes the spin. And the transformation of supersymmetry is just such a transformation. It reduces the spin of a particle by 1/2 and, therefore, can mix particles with different spins. Thus, combining with gravity within supersymmetry is quite natural.
Nature of dark matter of the universe
Supersymmetry may explain some of the results of research in cosmology. One of these results is that the visible (luminous) matter does not constitute all the matter in the Universe. A significant amount of energy comes from so-called dark matter and dark energy .
Direct evidence for the existence of dark matter is the dependence of the velocities of stars in spiral galaxies on their distance from the center. This dependence is easy to calculate. It turns out that the experimental data significantly differ from the predictions of the theory.
The discrepancy is explained by the fact that galaxies are in the "clouds" of dark matter. Dark matter particles interact only gravitationally. Therefore, they are grouped around galaxies (it would be more correct to say that ordinary matter is grouped around clumps of dark matter) and distort the mass distribution in the galaxy.
Relic radiation - the equilibrium thermal radiation filling the Universe. This radiation was separated from matter in the early stages of the expansion of the Universe, when electrons combined with protons and formed hydrogen atoms (recombination). Then the universe was 1000 times younger than it is now. The current temperature of the CMB is about 3 K.
Recent high-precision measurements of the temperature distribution of the CMB across the sky in the WMAP experiment showed that the total energy of the Universe is distributed between dark energy (73%), dark matter (23%) and ordinary matter (4%), that is, dark matter is a significant part, exceeding many times the proportion of visible matter.
There are no suitable particles in the Standard Model to explain dark matter. At the same time, in some supersymmetric models there is an excellent candidate for the role of cold dark matter, namely neutralino, the lightest supersymmetric particle. It is stable, so that relic neutralinos could persist in the Universe from the time of the Big Bang.
As for dark energy, its nature in the framework of modern physical theories is completely incomprehensible. This is a real challenge to the physicists of the twenty-first century. Dark energy can be interpreted as the self-energy of a vacuum, however, there are huge discrepancies between the theoretical estimates and the observed value of the density of dark energy. The existence of dark energy leads to observable consequences - accelerated expansion of the Universe at the present time.
MSSM
To build supersymmetric models, a mathematical apparatus was developed, to dwell on which there is no possibility. However, despite the complexity of the mathematical apparatus, supersymmetric theories have a number of simple features.
One of these features is the doubling of the number of particles. Each particle acquires a super-partner — a particle that has exactly the same properties, with the exception of the spin, which differs by 1/2.
In the Standard Model, there are no particles that could be each other's superpartners. Consequently, in the supersymmetric extensions of the Standard Model, each particle acquires its own super-partner — a new particle. The minimal supersymmetric Standard Model (MSSM) requires the least new particles to build.
Another important feature of supersymmetric models is the violation of supersymmetry. If there was no such violation, the superpartners would have the same mass as ordinary particles. However, new particles with masses of known particles of the Standard Model have never been observed. Also without the breaking of supersymmetry, the Higgs mechanism of breaking the electroweak symmetry would not work.
To apply supersymmetric models in high-energy physics, it is necessary to require a violation of supersymmetry. In this case, superpartners can acquire large masses, which can explain their non-observation at the present time.
The specific mechanism for breaking supersymmetry is currently unknown. This significantly reduces the predictive power of the model, since a large number of free parameters appear in it, choosing which one can get arbitrary consequences. Some considerations, such as the grand unification hypothesis, allow us to limit the number of free parameters. The study of restrictions on the parameters of supersymmetric models is one of the important directions in the study of physics beyond the Standard Model.
Experimental status of supersymmetric models
Supersymmetry is one of the main candidates for the role of a new theory in elementary particle physics beyond the framework of the Standard Model. The search for various manifestations of supersymmetry in nature has been one of the main objectives of numerous experiments at colliders (LEP - large electron-positron collider and Tevatron) and in non-accelerator experiments for several decades.
Unfortunately, the result is still negative. There are no direct indications of the existence of supersymmetry in particle physics, although the available supersymmetric models in general are not prohibited by the existing theoretical and experimental requirements.
LHC (Large Hadron Collider) is a new accelerator built at CERN. His energy is seven times the energy of the current American accelerator Tevatron. In most supersymmetric models, the masses of new particles lie in the region accessible by the LHC. It is assumed that the Higgs boson and supersymmetric particles will be discovered at the LHC. In new experiments, low-energy supersymmetry will be either detected or excluded.
Although supersymmetry is not open to experience, various supersymmetric models can be investigated now. First, it is necessary to exclude models in which new particles have insufficiently large masses, which have now been experimentally closed. Secondly, discrepancies between some experimental data and theoretical predictions of the Standard Model can be explained by the contribution of supersymmetric particles, and from this point of view some supersymmetric models are preferable to others.
Many specialists in high energy physics are exploring various options for supersymmetric models and their consequences. It is possible that one of these models will be confirmed on the LHC accelerator.
Source: https://habr.com/ru/post/100119/
All Articles